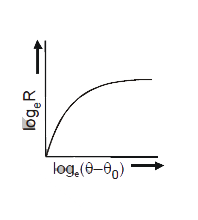
The curve between loge L and loge P is (L is the angular momentum and P is the linear momentum).




The correct Answer is:B
To solve the problem regarding the relationship between the logarithm of angular momentum (L) and the logarithm of linear momentum (P), we can follow these steps:
1. Understand the Relationship:
We start with the relationship between angular momentum (L) and linear momentum (P). The angular momentum L is given by the equation:
L=R×P
where R is the position vector and P is the linear momentum.
2. Express Angular Momentum:
The magnitude of angular momentum can also be expressed as:
L=RPsin(θ)
where θ is the angle between the position vector R and the linear momentum vector P.
3. Take the Natural Logarithm:
We take the natural logarithm of both sides:
loge(L)=loge(RPsin(θ))
4. Apply Logarithmic Properties:
Using the properties of logarithms, we can expand this:
loge(L)=loge(R)+loge(P)+loge(sin(θ))
5. Identify the Linear Relationship:
Rearranging the equation gives:
loge(L)=loge(P)+loge(R)+loge(sin(θ))
This can be written in the form of a linear equation:
y=mx+c
where:
- y=loge(L)
- x=loge(P)
- m=1 (the coefficient of x)
- c=loge(R)+loge(sin(θ)) (a constant)
6. Conclusion:
Since the relationship between loge(L) and loge(P) is linear, the graph of loge(L) versus loge(P) will be a straight line with a slope of 1 and a y-intercept equal to the constant c.
Final Answer
The curve between loge(L) and loge(P) is linear.
We start with the relationship between angular momentum (L) and linear momentum (P). The angular momentum L is given by the equation:
L=R×P
where R is the position vector and P is the linear momentum.
The magnitude of angular momentum can also be expressed as:
L=RPsin(θ)
where θ is the angle between the position vector R and the linear momentum vector P.
We take the natural logarithm of both sides:
loge(L)=loge(RPsin(θ))
Using the properties of logarithms, we can expand this:
loge(L)=loge(R)+loge(P)+loge(sin(θ))
Rearranging the equation gives:
loge(L)=loge(P)+loge(R)+loge(sin(θ))
This can be written in the form of a linear equation:
y=mx+c
where:
- y=loge(L)
- x=loge(P)
- m=1 (the coefficient of x)
- c=loge(R)+loge(sin(θ)) (a constant)
Since the relationship between loge(L) and loge(P) is linear, the graph of loge(L) versus loge(P) will be a straight line with a slope of 1 and a y-intercept equal to the constant c.
The curve between loge(L) and loge(P) is linear.
Topper's Solved these Questions
- SYSTEM OF PARTICLES & ROTATIONAL MOTION BOOK - DISHA PUBLICATIONCHAPTER - SYSTEM OF PARTICLES & ROTATIONAL MOTION EXERCISE - EXERCISE-2 : CONCEPT APPLICATOR
28 Videos
- SYSTEM OF PARTICLES & ROTATIONAL MOTION BOOK - DISHA PUBLICATIONCHAPTER - SYSTEM OF PARTICLES & ROTATIONAL MOTION EXERCISE - EXERCISE-2 : CONCEPT APPLICATOR
28 Videos
- SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - DISHA PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - EXERCISE -2: CONCEPT APPLICATOR
25 Videos
- THERMAL PROPERTIES OF MATTER BOOK - DISHA PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTER EXERCISE - Exercise-2 (Concept Applicator)
28 Videos
Similar Questions
Knowledge Check
The angular momentum of p electron is
Ah2π√6Bh√2Ch2π√2Dh√6The dimensions of the ratio of angular momentum to linear momentum is
A[M0LT0]B[MLT−1]C[ML2T−1]D[M−1L−1T−1]The correct curve between logeR and loge(θ−θo) is -
A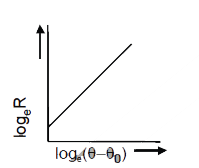 B
B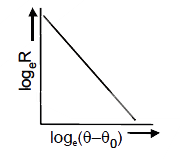 C
C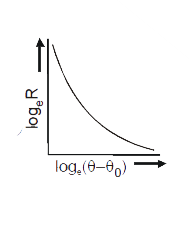 D
D