A uniform rod of length l is free to rotate in a vertical plane about a fixed horizontal axis through O. The rod begins rotating from rest from its unstable equilibrium position. When it has turned through an angle θ, its angular velocity ω is given as

√6glsinθ
√6glsin.θ2
√6glcos.θ2
√6glcosθ
The correct Answer is:C
12Iω2 = Loss of gravitational potental energy
12×ml23ω2=mgl2(1+cosθ)
⇒ω2=3gl(2cos2.θ2)⇒ω=√6glcos.θ2
Topper's Solved these Questions
- SYSTEM OF PARTICLES & ROTATIONAL MOTION BOOK - DISHA PUBLICATIONCHAPTER - SYSTEM OF PARTICLES & ROTATIONAL MOTION EXERCISE - EXERCISE-2 : CONCEPT APPLICATOR
28 Videos
- SYSTEM OF PARTICLES & ROTATIONAL MOTION BOOK - DISHA PUBLICATIONCHAPTER - SYSTEM OF PARTICLES & ROTATIONAL MOTION EXERCISE - EXERCISE-2 : CONCEPT APPLICATOR
28 Videos
- SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - DISHA PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - EXERCISE -2: CONCEPT APPLICATOR
25 Videos
- THERMAL PROPERTIES OF MATTER BOOK - DISHA PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTER EXERCISE - Exercise-2 (Concept Applicator)
28 Videos
Similar Questions

A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution
Knowledge Check

A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asA√(6gL)sin(θ2)B√(6gL)cos(θ2)C√(6gL)sinθD√(6gL)cosθAn L shaped thin uniform rod of total length 2l is free to rotate in a vertical plane about a horizontal axis a P as shown in the figure. The bas is released from rest. Neglect air and contact friction. The angular velociyt at the instant it has rotated through 90∘ and reached the dotted position shown is
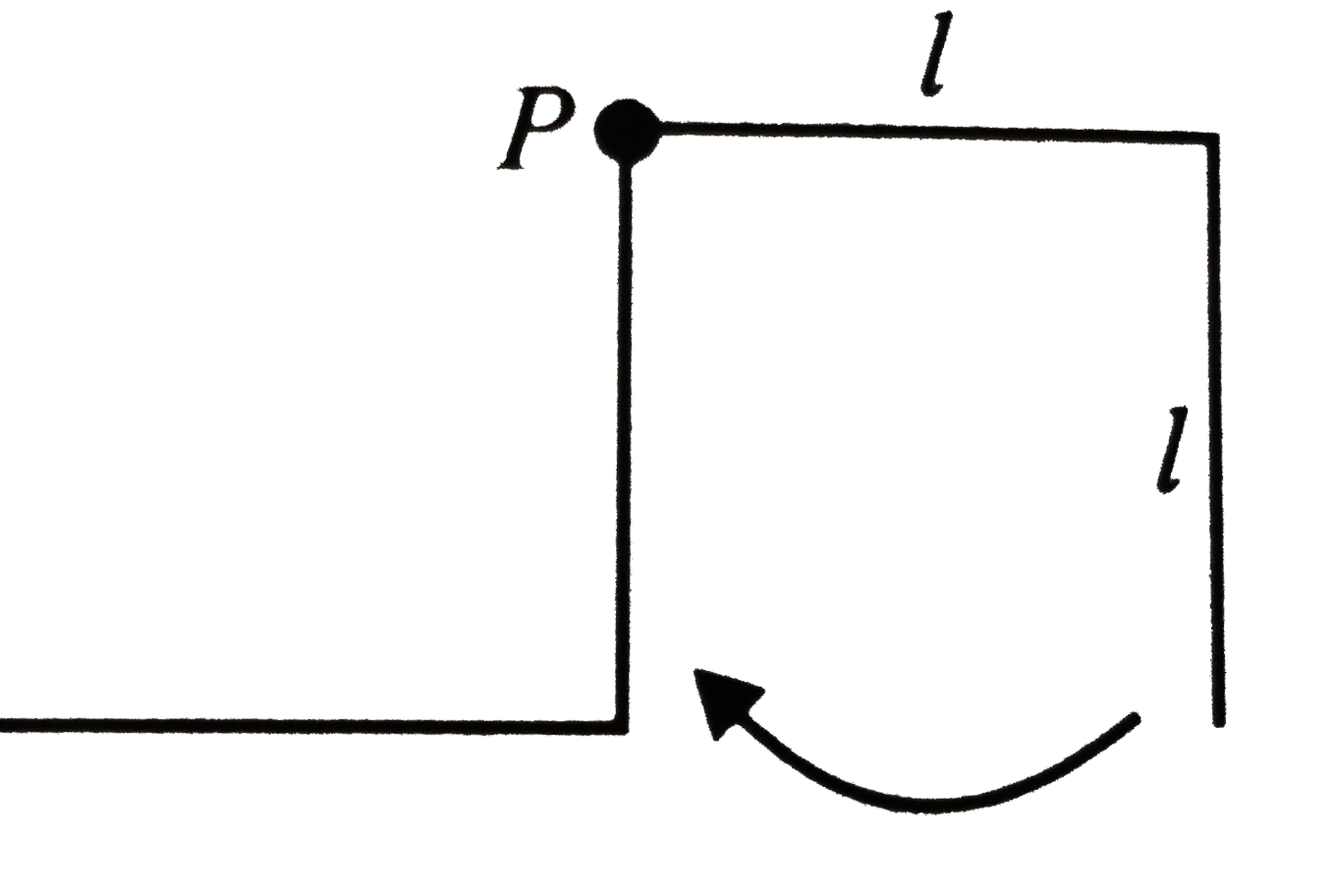 AzeroB√6g5lC√3g5lDnone
AzeroB√6g5lC√3g5lDnone
A uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA uniform rod of length L is free to rotate about an axis passing through O. Inititally the rod is horizontal. The rod is relased from this position. Match column I with column II
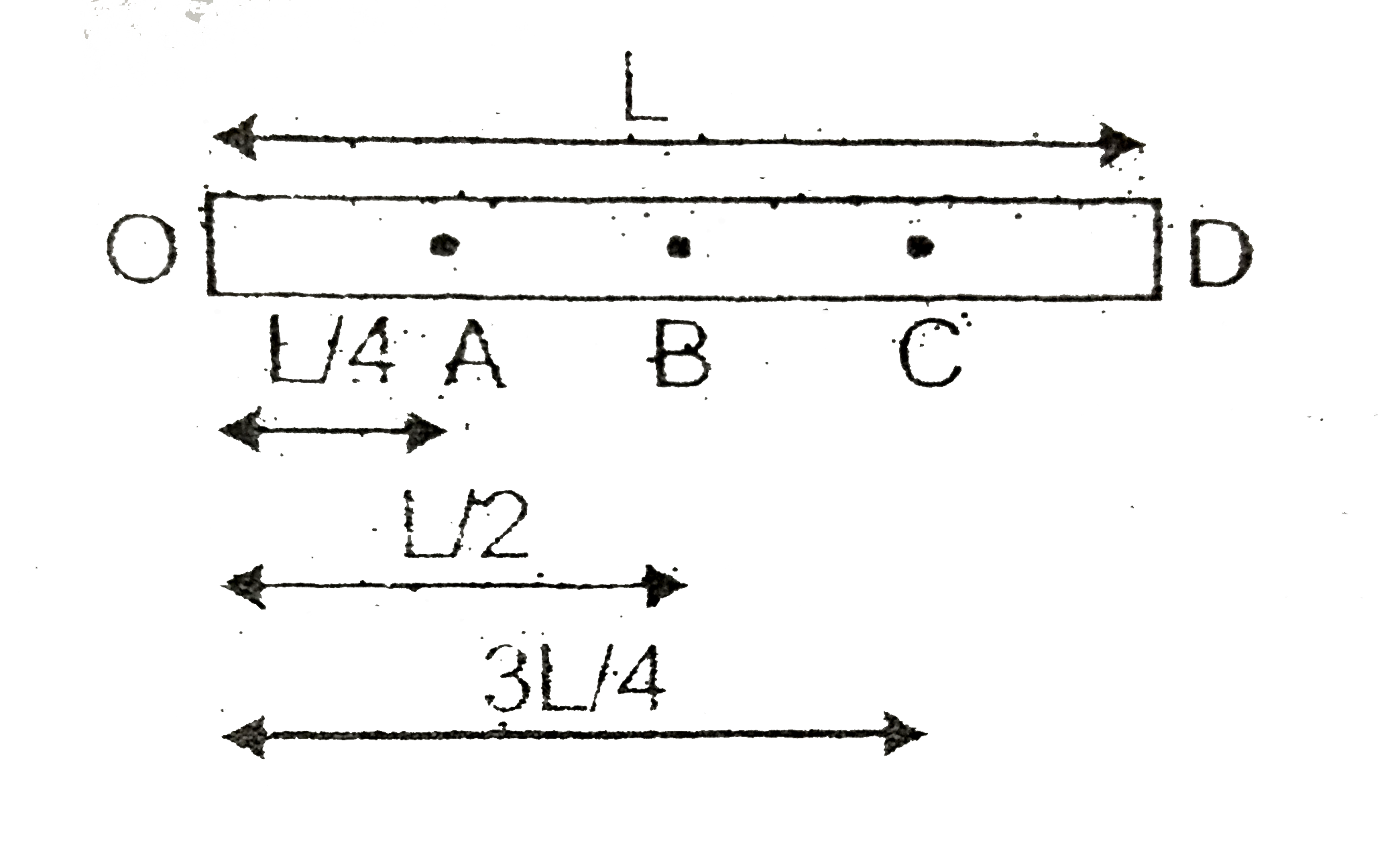
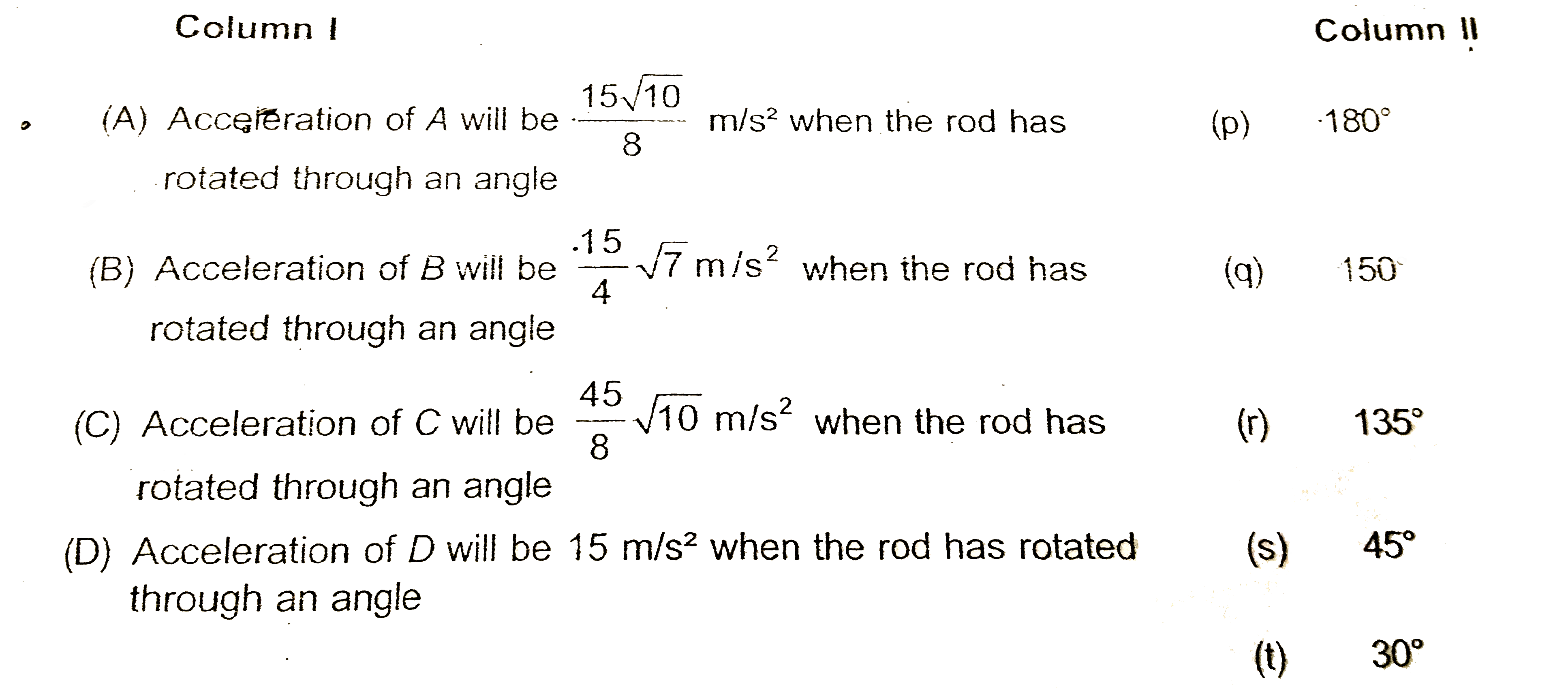
View SolutionA uniform rod of length L is free to rotate about an axis passing through O. Inititally the rod is horizontal. The rod is relased from this position. Match column I with column II

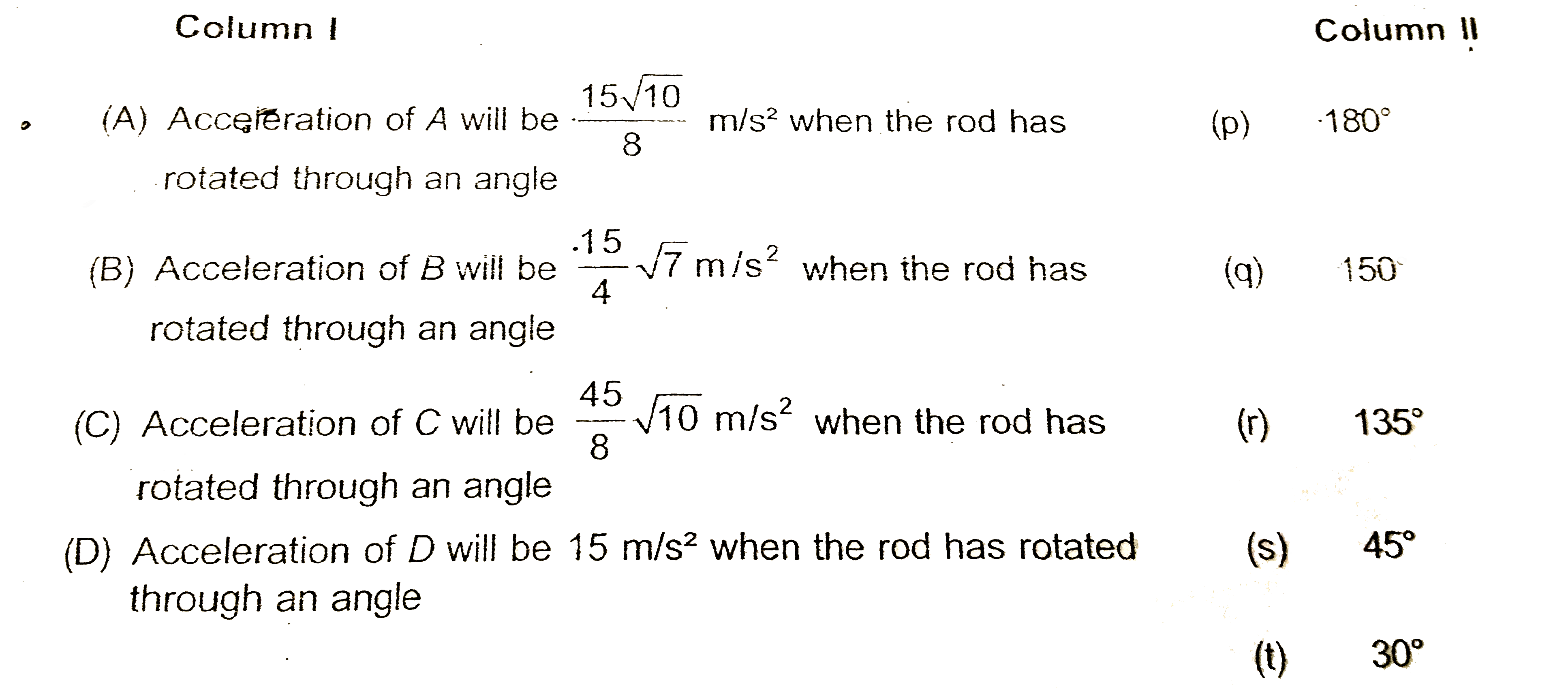
View SolutionA long uniform rod of length L, mass M is free to rotate in a horizontal plane about a vertical axis through its end. Two springs of constant K each are connected as shown. On equilibrium, the rod was horizontal. The frequency will be –
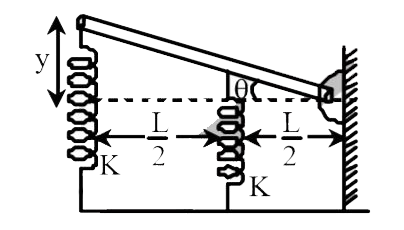
View SolutionAn L shaped thin uniform rod of total length 2l is free to rotate in a vertical plane about a horizontal axis a P as shown in the figure. The bas is released from rest. Neglect air and contact friction. The angular velociyt at the instant it has rotated through 90∘ and reached the dotted position shown is

View Solution
