The radius of a planet is n times the radius of earth (R). A satellite revolves around it in a circle of radius 4nR with angular velocity ω. The acceleration due to gravity on planet's surface is
Rω2
16 Rω2
32nRω2
64nRω2
The correct Answer is:D
To find the acceleration due to gravity on a planet whose radius is n times the radius of Earth, we can follow these steps:
1. Identify the formula for acceleration due to gravity (g):
The acceleration due to gravity at the surface of a planet is given by the formula:
g=G⋅MR2
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
2. Define the radius of the planet:
Given that the radius of the planet is n times the radius of Earth (R), we can express the radius of the planet as:
Rp=nR
3. Determine the mass of the planet:
The mass of the planet can be expressed in terms of its density (ρ) and volume. The volume V of a sphere is given by:
V=43πR3
Therefore, the mass of the planet is:
Mp=ρ⋅V=ρ⋅43π(nR)3=ρ⋅43πn3R3
4. Substitute the mass into the gravity formula:
Now substituting Mp into the formula for g:
g=G⋅(ρ⋅43πn3R3)(nR)2
5. Simplify the expression:
Simplifying the expression:
g=G⋅ρ⋅43πn3R3n2R2
g=G⋅ρ⋅43πn3Rn2
g=43⋅G⋅ρ⋅n3
6. Relate to the satellite's motion:
We know that the satellite is revolving around the planet at a radius of 4nR with angular velocity ω. The centripetal acceleration a for the satellite is given by:
a=ω2r
where r=4nR. Thus,
a=ω2(4nR)=4nRω2
7. Set gravitational force equal to centripetal force:
The gravitational force acting on the satellite can also be expressed as:
F=G⋅Mp⋅ms(4nR)2
Setting the gravitational force equal to the centripetal force gives:
G⋅Mp⋅ms(4nR)2=ms⋅4nRω2
Canceling ms and rearranging gives:
G⋅Mp=16n2R2ω2
8. Substituting for Mp:
Substitute Mp=ρ⋅43πn3R3 into the equation:
G⋅(ρ⋅43πn3R3)=16n2R2ω2
9. Final expression for g:
Now substituting back into the formula for g:
g=G⋅MpR2p=G⋅(ρ⋅43πn3R3)(nR)2
Simplifying gives:
g=64ω2nRn2=64ω2R
Final Answer:
The acceleration due to gravity on the planet is:
g=64ω2nR
The acceleration due to gravity at the surface of a planet is given by the formula:
g=G⋅MR2
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
Given that the radius of the planet is n times the radius of Earth (R), we can express the radius of the planet as:
Rp=nR
The mass of the planet can be expressed in terms of its density (ρ) and volume. The volume V of a sphere is given by:
V=43πR3
Therefore, the mass of the planet is:
Mp=ρ⋅V=ρ⋅43π(nR)3=ρ⋅43πn3R3
Now substituting Mp into the formula for g:
g=G⋅(ρ⋅43πn3R3)(nR)2
Simplifying the expression:
g=G⋅ρ⋅43πn3R3n2R2
g=G⋅ρ⋅43πn3Rn2
g=43⋅G⋅ρ⋅n3
We know that the satellite is revolving around the planet at a radius of 4nR with angular velocity ω. The centripetal acceleration a for the satellite is given by:
a=ω2r
where r=4nR. Thus,
a=ω2(4nR)=4nRω2
The gravitational force acting on the satellite can also be expressed as:
F=G⋅Mp⋅ms(4nR)2
Setting the gravitational force equal to the centripetal force gives:
G⋅Mp⋅ms(4nR)2=ms⋅4nRω2
Canceling ms and rearranging gives:
G⋅Mp=16n2R2ω2
Substitute Mp=ρ⋅43πn3R3 into the equation:
G⋅(ρ⋅43πn3R3)=16n2R2ω2
Now substituting back into the formula for g:
g=G⋅MpR2p=G⋅(ρ⋅43πn3R3)(nR)2
Simplifying gives:
g=64ω2nRn2=64ω2R
The acceleration due to gravity on the planet is:
g=64ω2nR
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE-230videos
GRAVITATION
- BOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE-230videos
GRAVITATION
- BOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE 2: CONCEPT APPLICATOR24videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - DISHA PUBLICATIONCHAPTER - JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))EXERCISE - QUESTIONS30videos
JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))
Similar Questions
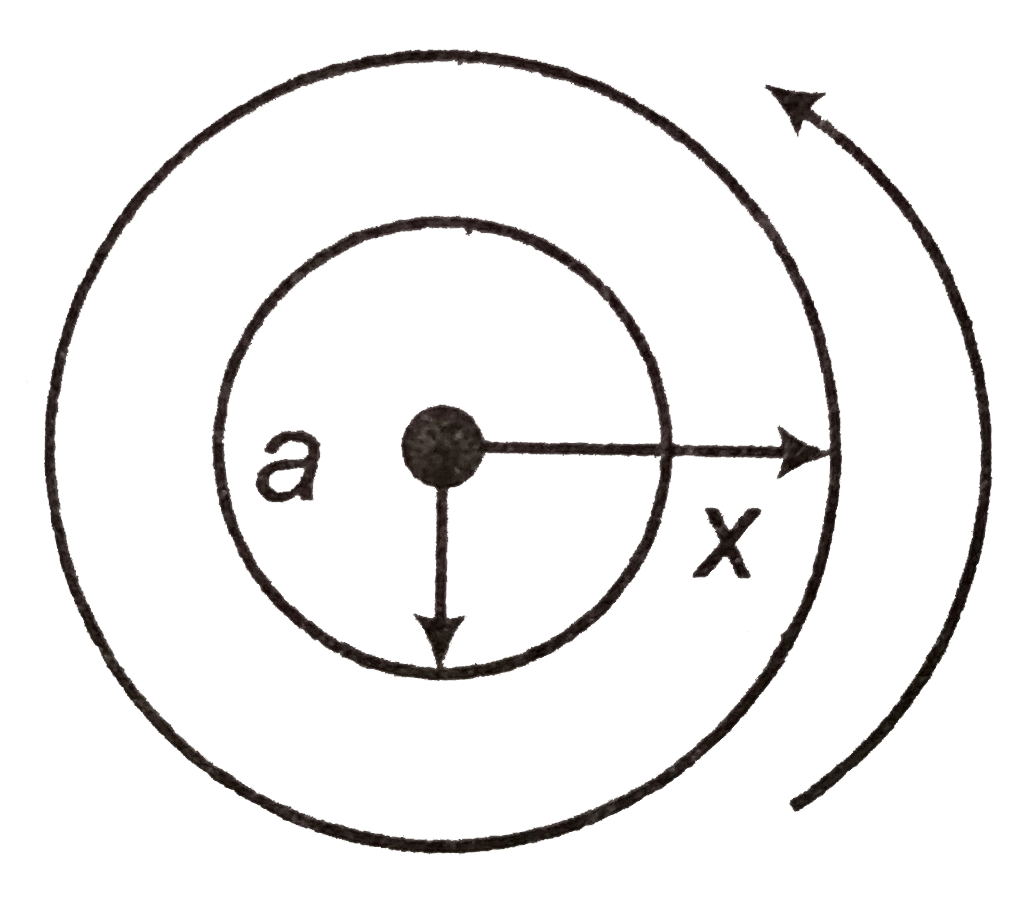
The radius of a planet is a. satelite revolves around it in a circle of radius x with angular velocity ω. The acceleration due to the gravity on planet's surface isView SolutionThe radius ofa planet is R1and a satellite revolves round it in a circle of radius R2. The tiemperiod of revolution is T. find the acceleration due to the gravitational of the plane at its surface.
View Solution
Knowledge Check
- Question 1 - Select One
The radius of a planet is R. A satellite revolves around it in a circle of radius r with angular velocity ω0. The acceleration due to the gravity on planet's surface is
Ar3ω0RBr3ω20R2Cr3ω20RDr3ω20R2 - Question 2 - Select One
A planet has a mass of eight time the mass of earth and denisity is also equal to eight times a the average density of the earth. If g be the acceleration due to earth's gravity on its surface, then acceleration due to gravity on planet's surface will be
A2gB4gC8gD16g - Question 3 - Select One
Periodic time of a satellite revolving above Earth's surface at a height equal to R, radius of Earth, is : [g is acceleration due to gravity at Earth's surface]
A2πr√2RgB4√2π√RgC2π√RgD8π√Rg
The mass of a planet is twice the mass of earth and diameter of the planet is thrie the diameter of the earth, then the acceleration due to gravity on the planet's surface is
View SolutionIf R denotes the radius of orbit of a satellite of mass m revolving around a planet of mass M, the sqiared orbital velocity of the satellite is given by
View SolutionThe escape velocity of a body at the surface of planet P is 1√5 times than that at surface of earth. The radius of planet is 124 times the radius of earth. The acceleration due to gravity for planet is
View SolutionA planet has density p, radius R and acceleration due to gravity as g. If the radius of the planet were doubled keeping the density same, the acceleration due to gravity at the surface will be
View SolutionThe radius of a planet is 14 of earth’s radius and its acceleration due to gravity is double that of earth’s acceleration due to gravity. How many times will the escape velocity at the planet’s surface be as compared to its value on earth’s surface
View Solution

