The gravitational field, due to the 'left over part' of a uniform sphere (from which a part as shown , has been 'removed out') at a very far off point, P , located as shown, would be (nearly) :
(##DSH_NTA_JEE_MN_PHY_C07_E03_008_Q01.png" width="80%">
56GMx2
89GMx2
78GMx2
67GMx2
The correct Answer is:C
Let mass of smaller sphere (which has to be removed ) is m
Radius = R2 (from figure)
M43πR3=m43π(R2)3⇒m=M8
Mass of the left over part of the sphere
M.=M−M8=78 M
therefore gravitational field due to the left over part of the sphere
=GM.x2−78GMx2
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE -160videos
GRAVITATION
- BOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE 2: CONCEPT APPLICATOR24videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - DISHA PUBLICATIONCHAPTER - JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))EXERCISE - QUESTIONS30videos
JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))
Similar Questions
Knowledge Check
- Question 1 - Select One
The reaction of CH3CH=
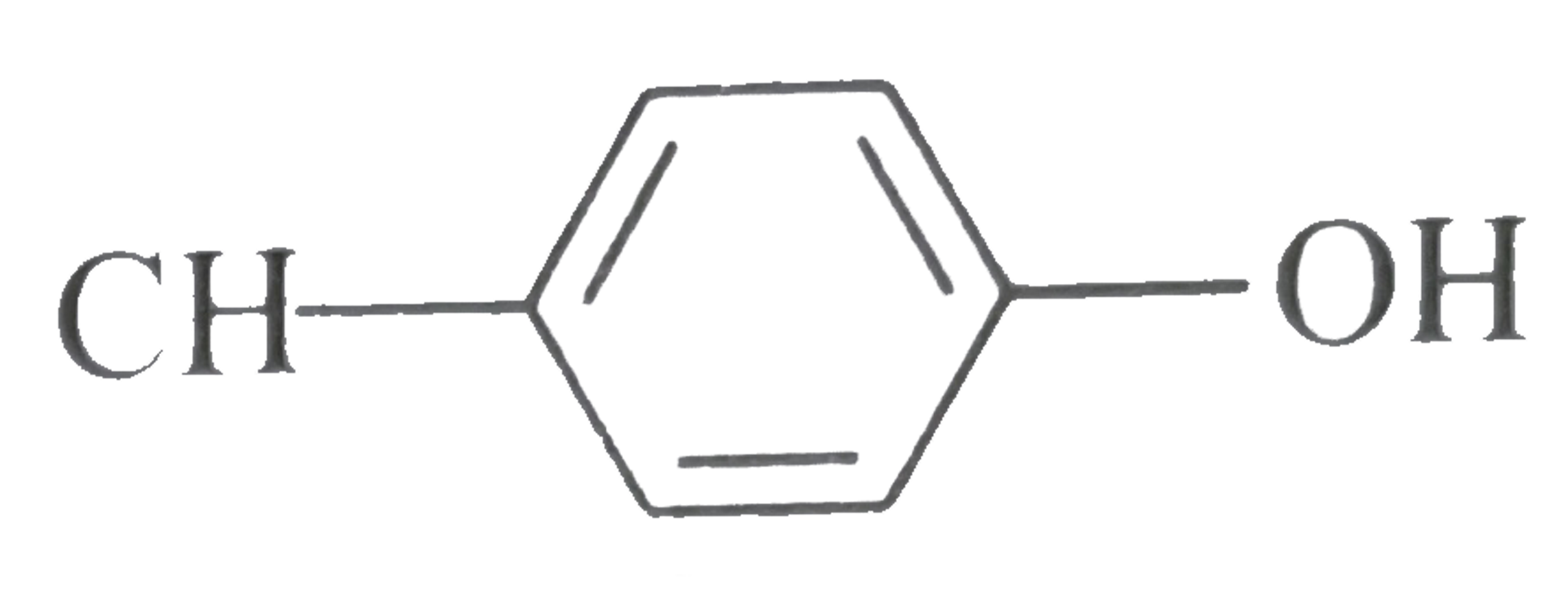with HBr givesACH_(3)CHBrCH_(2) (##DSH_NTA_JEE_MN_CHE_C13_E02_042_O01.png" width="30%">BCH_(3)CH_(2)CHBr (##DSH_NTA_JEE_MN_CHE_C13_E02_042_O02.png" width="30%">CCH_(3)CHBrCH_(2) (##DSH_NTA_JEE_MN_CHE_C13_E02_042_O03.png" width="30%">DCH_(3)CH_(2)Br (##DSH_NTA_JEE_MN_CHE_C13_E02_042_O04.png" width="30%"> - Question 2 - Select One
The reagent needed for converting
Ph - C -= C - Ph to (##DSH_NTA_JEE_MN_CHE_C13_E01_014_Q01.png" width="80%"> is :ACat . HydrogenationBH2/Lindlar Cat .CLi/NH3DLiAlH4 - Question 3 - Select One
Two hypothetical planets of masses m1andm2 are at rest when they are infinite distance apart. Because of the gravitational force they move towards each other along the line joining their centres. What is their speed when their separation is 'd' ?
(speed of m1 is v1 and that of m2 is v2)
(##DSH_NTA_JEE_MN_PHY_C07_E03_021_Q01.png" width="80%">Av1=v2Bv1=m2√2Gd(m1+m2) v2=−m1√2Gd(m1+m2)Cv1=m1√2Gd(m1+m2) v2=m2√2Gd(m1+m2)Dv1=m2√2Gm1 v2=m1√2Gm2
Find the effective resistance between points A and B for the network shown in the figure below.
(ARH_NEET_PHY_OBJ_V02_C03_S01_027_Q01.png" width="80%">View SolutionFour masses are fixed on a mass less rod as shown in Fig . The moment of inertia about the axis P is about :
(##NAR_NEET_PHY_XI_P2_C05_E06_024_Q01.png" width="80%">View SolutionFrom a sphere of mass M and radius R, a smaller sphere of radius R2 is carved out such that the cavity made in the original sphere is between its centre and the periphery (see figure. ) for the configuration in the figure where the distance between the centre of the original sphere and the removed sphere is 3R, the gravitational force between the two sphere is :
(##DSH_NTA_JEE_MN_PHY_C07_E01_012_Q01.png" width="80%">View SolutionAn object is placed near two perpendicular plane mirrors as shown in the figure.How many images will be formed?
(##MST_AG_JEE_MA_PHY_V02_C33_E01_030_Q01.png" width="80%">View SolutionIndia's Mangalyan was sent to the Mars by launching it into a transfer orbit EOM around then sun. It leaves the earth at E and meets Mars at M. If the semi-major axis of Earth's orbit is ae=1.5×1011 m, that of Mars orbit am=2.28×1011 m , take Kepler's laws give the estimate of time for Mangalyan to reach Mars from Earth to be close to :
(##DSH_NTA_JEE_MN_PHY_C07_E01_008_Q01.png" width="80%">View Solution