Unit mass of liquid of volume V1 completely turns into a gas of volume V2 at constant atmospheric pressure P and temperature T. The latent heat of vaporization is "L". Then the change in internal energy of the gas is
zero
P(V2−V1)
L−P(V2−V1)
L
The correct Answer is:C
Q=mL=1×L=L,W=P(V2−V1)
Now Q=ΔU+W
or L=ΔU+P(V2−V1)
∴ΔU=L−P(V2−V1)
Topper's Solved these Questions
- THERMODYNAMICS BOOK - DISHA PUBLICATIONCHAPTER - THERMODYNAMICS EXERCISE - EXERCISE-1 : CONCEPT BUILDER (Topic-3 CARNOT ENGINE, REFIGERATOR AND SECOND LAW OF THERMODYNAMICS)
15 Videos
- THERMODYNAMICS BOOK - DISHA PUBLICATIONCHAPTER - THERMODYNAMICS EXERCISE - EXERCISE -2 : CONCEPT APPLICATOR
29 Videos
- THERMODYNAMICS BOOK - DISHA PUBLICATIONCHAPTER - THERMODYNAMICS EXERCISE - EXERCISE-1 : CONCEPT BUILDER (Topic- ZEROTH LOW AND FIRST LAW OF THERMODYNAMICS)
11 Videos
- THERMAL PROPERTIES OF MATTER BOOK - DISHA PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTER EXERCISE - Exercise-2 (Concept Applicator)
28 Videos
- WAVE OPTICSBOOK - DISHA PUBLICATIONCHAPTER - WAVE OPTICSEXERCISE - EXERCISE-2 : CONCEPT APPLICATOR
30 Videos
Similar Questions
Two moles of a gas at temperature T and volume V are heated to twice its volume at constant pressure. If CpCv=γ then increase in internal energy of the gas is-
View SolutionTwo moles of an ideal monatomic gas, initially at pressure p1 and volume V1, undergo an adiabatic compression until its volume is V2. Then the gas is given heat Q at constant volume V2.
(i) Sketch the complete process on a p-V diagram.
(b) Find the total work done by the gas, the total change in its internal energy and the final temperature of the gas. [Give your answer in terms of p1,V1,V2,QandR]
View Solution
Knowledge Check
An ideal gas has a volume of 3V at 2 atmosphere pressure. Keeping the temperature constant. Its pressure is doubled. The volume of the gas will be
A6VB3VC1.5VD1VWhen volume changes from V to 2V at constant pressure(P) then the change in internal energy will be:
APVB3PVCPVγ−1DRVγ−1A monoatomic gas of n -moles is heated from temperature T to T under two different conditions (i) at constant volume and (ii) at constant pressure. The change in internal energy of the gas is
AMore forBMore for (ii)CSame in both casesDIndependent of number of moles
The pressure and volume of a gas changed as shown in the P-V diagram in this figure. The temperature of the gas will
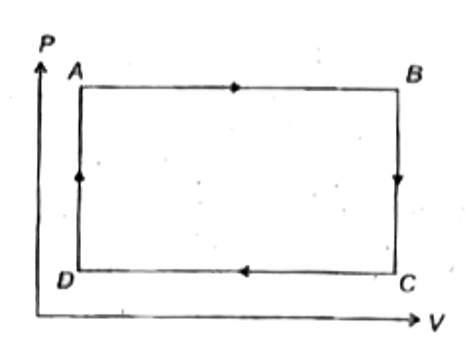
View SolutionTwo moles of a gas at temperature T and volume V are heated to twice its volume at constant pressure. If CpCv=γ then increase in internal energy of the gas is-
View SolutionA monoatomic gas of n-moles is heated temperature T1 to T2 under two different conditions
(i) at constant volume and
(ii) At constant pressure The change in internal energy of the gas is
View SolutionA monoatomic gas at a temperature T has pressure P and heat energy per unit volume E. then
View SolutionThe amount of heat required to raise the temperature of a diatomic gas by 1ºC at constant pressure is Qp and at constant volume is Qv. The amount of heat which goes as internal energy of the gas in the two cases is nearly
View Solution
