A block of mass m is kept on smooth horizontal surface and connected with two springs as shown in figure. Initially springs are in their natural length. Time period of small horizontal oscillation of the block is :

2π√mk
2π√m5k
π√mk
(π+2√3)√mk
The correct Answer is:C
When block is displaced slightly by x slightly towards right then x.=xcos30∘.
The restoring force
F=−(kx+4kx.cos30∘)
=−[kx+4k(xcos30∘)cos30∘]
=−[kx+3kx]=−4kx.
a=Fm=4km(−x)

On comparing with a=ω2x, we get
ω=√4km and T=2π√m4k=π√mk.
Topper's Solved these Questions
- OSCILLATIONS BOOK - DISHA PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Exercise-1 : Concept Builder (TOPIC 3: Damped & Forced Oscillations and Resonance)
11 Videos
- OSCILLATIONS BOOK - DISHA PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Exercise-2 : Concept Applicator
28 Videos
- OSCILLATIONS BOOK - DISHA PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Exercise-1 : Concept Builder (TOPIC 1: Displacement, Phase, Velocity, Acceleration and Energy in S.H.M.)
27 Videos
- NUCLEIBOOK - DISHA PUBLICATIONCHAPTER - NUCLEIEXERCISE - EXERCISE - 2 (CONCEPT APPLICATOR)
30 Videos
- PHYSICAL WORLD, UNITS AND MEASUREMENTSBOOK - DISHA PUBLICATIONCHAPTER - PHYSICAL WORLD, UNITS AND MEASUREMENTSEXERCISE - Exercise - 2 : Concept Applicator
30 Videos
Similar Questions
A block of mass m lie on a horizontal smooth surface and connected with the springs at their natural length as shown in figure. When block slightly displaced then find the time period of oscillation.

View SolutionA block of mass M is kept on a smooth surface and touches the two springs as shown in the figure but not attached to the springs. Initially springs are in their natural length. Now, the block is shifted (l0/2) from the given position in such a way that it compresses a spring and released. The time - period of oscillation of mass will be

View Solution
Knowledge Check
A block of mass M is kept on a smooth surface and touches the two springs as shown in the figure but not attached to the springs. Initially springs are in their natural length. Now, the block is shifted (l0/2) from the given position in such a way that it compresses a spring and released. The time - period of oscillation of mass will be
 Aπ2√MkB2π√M5kC3π2√MkDπ√M2k
Aπ2√MkB2π√M5kC3π2√MkDπ√M2kA block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2kA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
Two blocks A and B of masses m & 2m placed on smooth horizontal surface are connected with a light spring. The two blocks are given velocities as shown when spring is at natural length.
(i) Find velocity of centre of mass (b) maximum extension in the spring

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionTwo blocks rest on a smooth horizontal surface. They are connected by a spring of force constant k. If the system is set into oscillation find its time period.

View SolutionTwo blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
View SolutionA block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
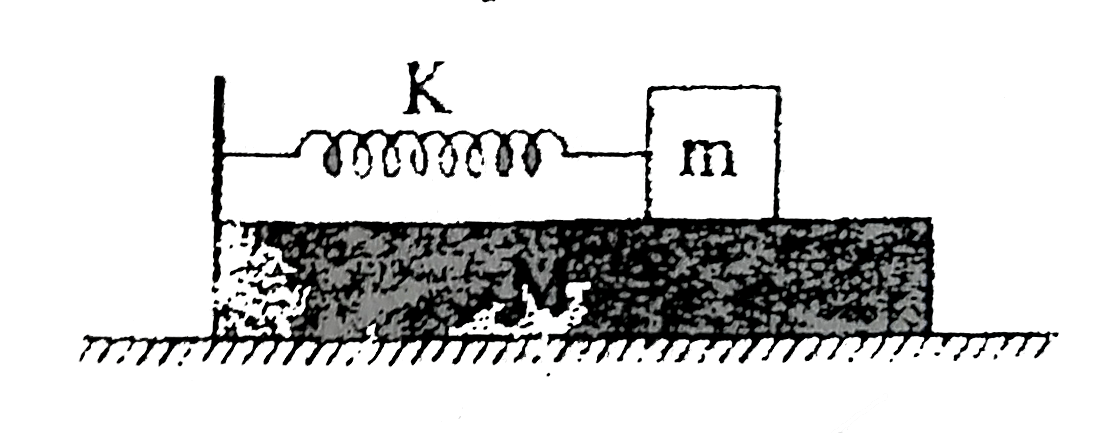
View Solution
