A sinusoidal voltage V(t)=100sin(500t) is applied across a pure inductance of L=0.02H. The current through the coil is :
A
10 cos (500 t)
B
−10cos(500t)
C
10sin(500t)
D
−10sin(500t)
Video Solution
Text Solution
The correct Answer is:B
In a pure inductive circuit current always lags behind the emf by π2
If v(t) = v0sinωt
then I=I0sin(ωt−π2)
Now, given v(t)=100sin(500t)
and I0=E0ωL=100500×0.02[∵L=0.02H]
I0=10sin(500t−π2)⇒I0=−10cos(500t)
|
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - DISHA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Exercise - 1 : CONCEPT BUILDER (TOPIC 1: Alternating Current, Voltage and Power)
20 Videos
- ALTERNATING CURRENT BOOK - DISHA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Exercise - 1 : CONCEPT BUILDER (Topic 2: A.C Circuits and Power Factor)
31 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
Similar Questions
Knowledge Check
A sinusoidal voltage V(t) = 100 sin (500t) is applied across a pure inductance of L = 0.02 H. the current through the coil is
A10 cos (500t).B−10 cos (500t).C10 sin (500t)D−10 sin (500t)A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
ACurrent l(t) leads voltage V(t) by 180∘BCurrent l(t) lags voltage V(t) by 90∘COver a full cycle the capacitor C does not consume any energy from the voltage sourceDCurrent l(t) is in phase with voltage V(t)If an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be
AI=I0sinωtBI=I0sin(ωt+π/2)CI=I0sin(ωt+π/2)DI=I0sin(ωt+π)
If an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be
View SolutionA small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
View SolutionAn alternating voltage E=E0sinωt , is applied across a coil of inductor L. The current flowing through the circuit at any instant is
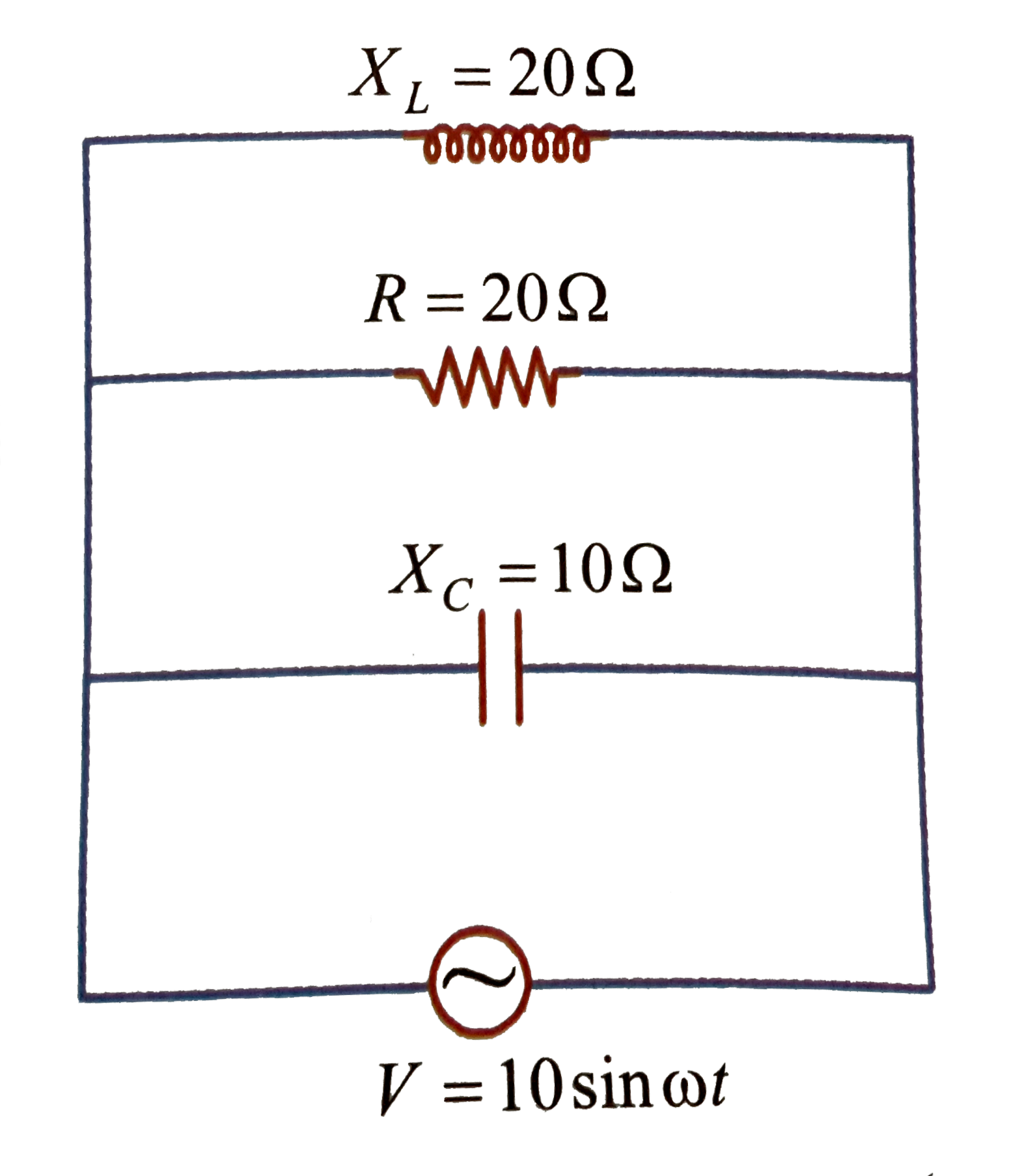
View SolutionAn alternative voltage V=10sinωt (in volts) is applied across a parallel arrangement as shown current (in A) through the source is best described by
View SolutionA sinusoidal voltage Vsin(at) is applied across a series combination of resistance R and inductor L. The amplitude of the current in the circuit is
View Solution
