An inductance L having a resistance R is connected to an alternating source of angular frequency ω.The quality factor Q of the inductance is
RωL
(ωLR)2
(RωL)12
ωLR
The correct Answer is:D
To find the quality factor Q of an inductance L having resistance R connected to an alternating source of angular frequency ω, we can follow these steps:
Step 1: Understand the Definition of Quality Factor
The quality factor Q is defined as the ratio of the voltage across the inductor VL to the voltage across the resistance VR.
Step 2: Express the Voltages
For an inductor, the voltage across it can be expressed as:
VL=I⋅XL
where I is the current through the circuit and XL is the inductive reactance given by:
XL=ωL
For the resistance R, the voltage across it is:
VR=I⋅R
Step 3: Write the Expression for Quality Factor
Now, substituting the expressions for VL and VR into the definition of Q:
Q=VLVR=I⋅XLI⋅R
Step 4: Simplify the Expression
The current I cancels out from the numerator and denominator:
Q=XLR
Step 5: Substitute the Inductive Reactance
Now, substituting XL=ωL into the equation:
Q=ωLR
Final Answer
Thus, the quality factor Q of the inductance is:
Q=ωLR
---
The quality factor Q is defined as the ratio of the voltage across the inductor VL to the voltage across the resistance VR.
For an inductor, the voltage across it can be expressed as:
VL=I⋅XL
where I is the current through the circuit and XL is the inductive reactance given by:
XL=ωL
VR=I⋅R
Now, substituting the expressions for VL and VR into the definition of Q:
Q=VLVR=I⋅XLI⋅R
The current I cancels out from the numerator and denominator:
Q=XLR
Now, substituting XL=ωL into the equation:
Q=ωLR
Thus, the quality factor Q of the inductance is:
Q=ωLR
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Exercise - 1 : CONCEPT BUILDER (Topic 3 : Transformers and LC Oscillations)19videos
ALTERNATING CURRENT
- BOOK - DISHA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Exercise -2 : Concept Applicator30videos
ALTERNATING CURRENT
- BOOK - DISHA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Exercise - 1 : CONCEPT BUILDER (TOPIC 1: Alternating Current, Voltage and Power)20videos
ALTERNATING CURRENT
- BOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR30videos
ATOMS
Similar Questions
An inductor has a resistance R and inductance L .It is connected to an A.C source of e.m.f E_(v) and angular frequency omega , then the current I_(v) in the circuit is
View SolutionA coil of inductance L=5/8H and of resistance R=62.8(Ω) is connected to the mains alternating voltage of frequency 50 Hz. What can be the capacitance of the capacitor (∈(μ)F) connected in series with the coil if the power dissipated has to remain unchanged? Take (π)2=10.
View Solution
Knowledge Check
- Question 1 - Select One
A wire of reistance R is connected in series with an inductor of reactance ω L. Then quality factor of RL circuit is
ARωLBωLRCR√R2+ω2L2DωL√R2+ω2L2 - Question 2 - Select One
A coil of inductance L=0.2 H and of resistance R=62.8Ω is connected to the mains alternating voltage of frequency 50Hz. What can be the capacitance of the capacitor connected in series with the coil if the useful power has to remain unchanged?
A10μCB50μCC25μCD100μC - Question 3 - Select One
An inductance L and capacitance C and resistance R are connected in series across an AC source of angular frequency ω. If ω2>1LC then
Aemf leads the currentBboth the emf and the current are in phaseCcurrent lead the emfDemf lags behind the current
Resistor of resistance R and capacitor of capacitance C are connected in series to an AC source of angular frequency ω . Rms current in the circuit is I. When frequency of the source is changed to one - third of initial value keeping the voltage same then current is found to be halved. Find the ratio of reactance of capacitor to that with resistance at the original frequency ω .
View SolutionA series LCR circuit having resistance R, capacitance C and inductance L has a voltage source of angular frequency ω and voltage V∈. Output voltage (Vout) is taken as voltage across the resistor and inductor combined.
(a) Find η=VoutVin
(b) Find η in the limit of large ω(ω>>1RC,1√LC,RL)
(C )Find η in the limit of smallω(ω>>1RC,1√LC,RL)
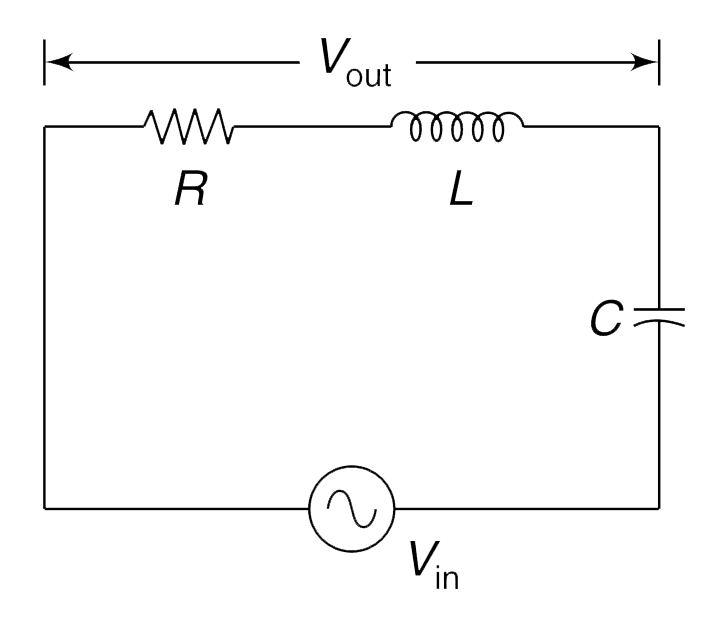 View Solution
View SolutionAn inductor has a resistance R inductance L. It is connected to an A.C source of e.m.f. EV and angular frequency ω then the current Iv in the circuit is
View SolutionAn LCR series circuit with 100 Ω resistance is connected to an ac source of 200 V and angular frequency 300 rad/s. When only the capacitance is removed, the current lags behind the voltage by 60∘. When only the inductance is removed, the current leads the voltage by 60∘.
When capacitor is removed, inductive reactance of the circuit isView SolutionAn inductor of inductance L and ressistor of resistance R are joined in series and connected by a source of frequency ω. Power dissipated in the circuit is
View Solution

