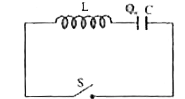
At t<0, the capacitor is charged and the switch is opened.At t=0 the switch is closed.The shortest time T at which the charge on the capacitor will be zero is given by:
A
π√LC
B
32π√LC
C
π2√LC
D
2π√LC
Text Solution
The correct Answer is:C
The time period of LC oscillations T=2π√LC
The time at which charge on the capactior will be zero is T4 . So, t=π2√LC
|
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - DISHA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Exercise -2 : Concept Applicator
30 Videos
- ALTERNATING CURRENT BOOK - DISHA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Exercise - 1 : CONCEPT BUILDER (Topic 2: A.C Circuits and Power Factor)
31 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
Similar Questions
Knowledge Check
In the circuit shown in figure, the capacitor is charged with a cell of 5V.If the switch is closed at t=0, then at t=12s, charge on the capacitor is
 A(0.37)10μCB(0.37)210μCC(0.63)10μCD(0.63)210μC
A(0.37)10μCB(0.37)210μCC(0.63)10μCD(0.63)210μCThe switch shown n the figure is closed at t=0. The charge on the capacitor as a function of time is given by
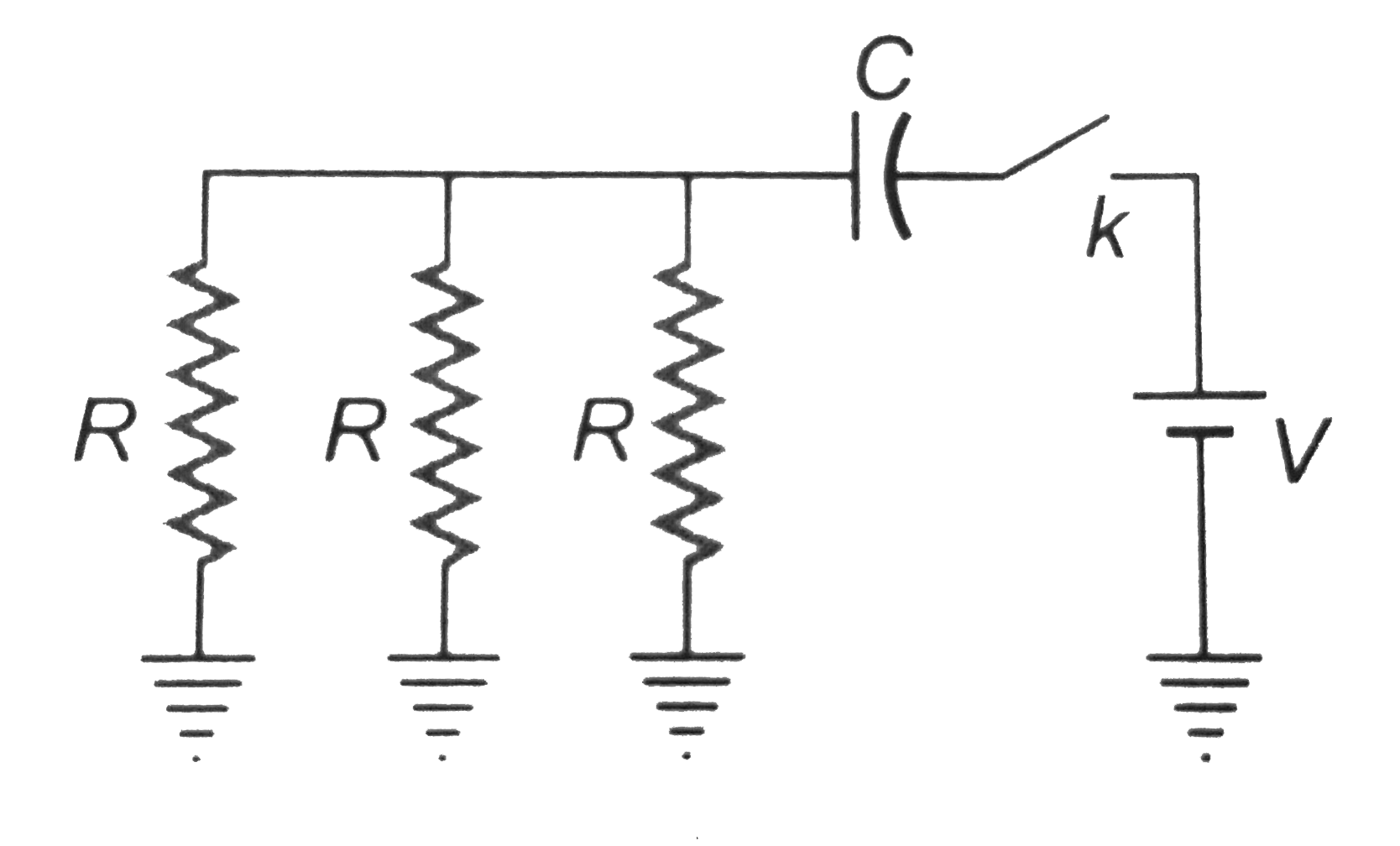 ACV(1−e−tRC)B3CV(1−e−tRC)CCV(1−e−3tRC)DCV(1−e−t3RC)
ACV(1−e−tRC)B3CV(1−e−tRC)CCV(1−e−3tRC)DCV(1−e−t3RC)In given circuit, switch S is closed at t=0 . The charge on the capacitor ar steady state will be
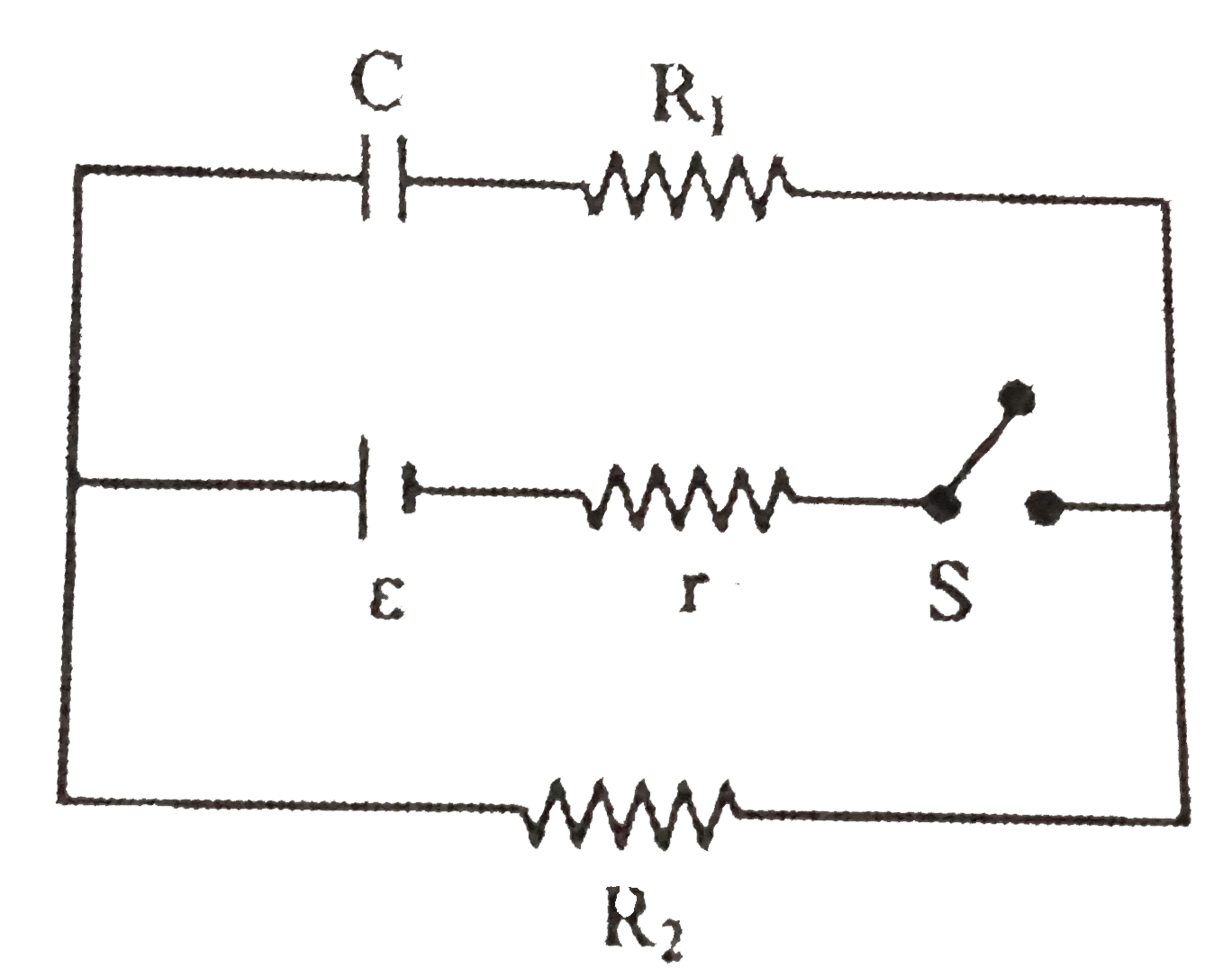 ACεR1r+R1BCεR2r+R2CCεR2r+R1DCεR1r+R2
ACεR1r+R1BCεR2r+R2CCεR2r+R1DCεR1r+R2
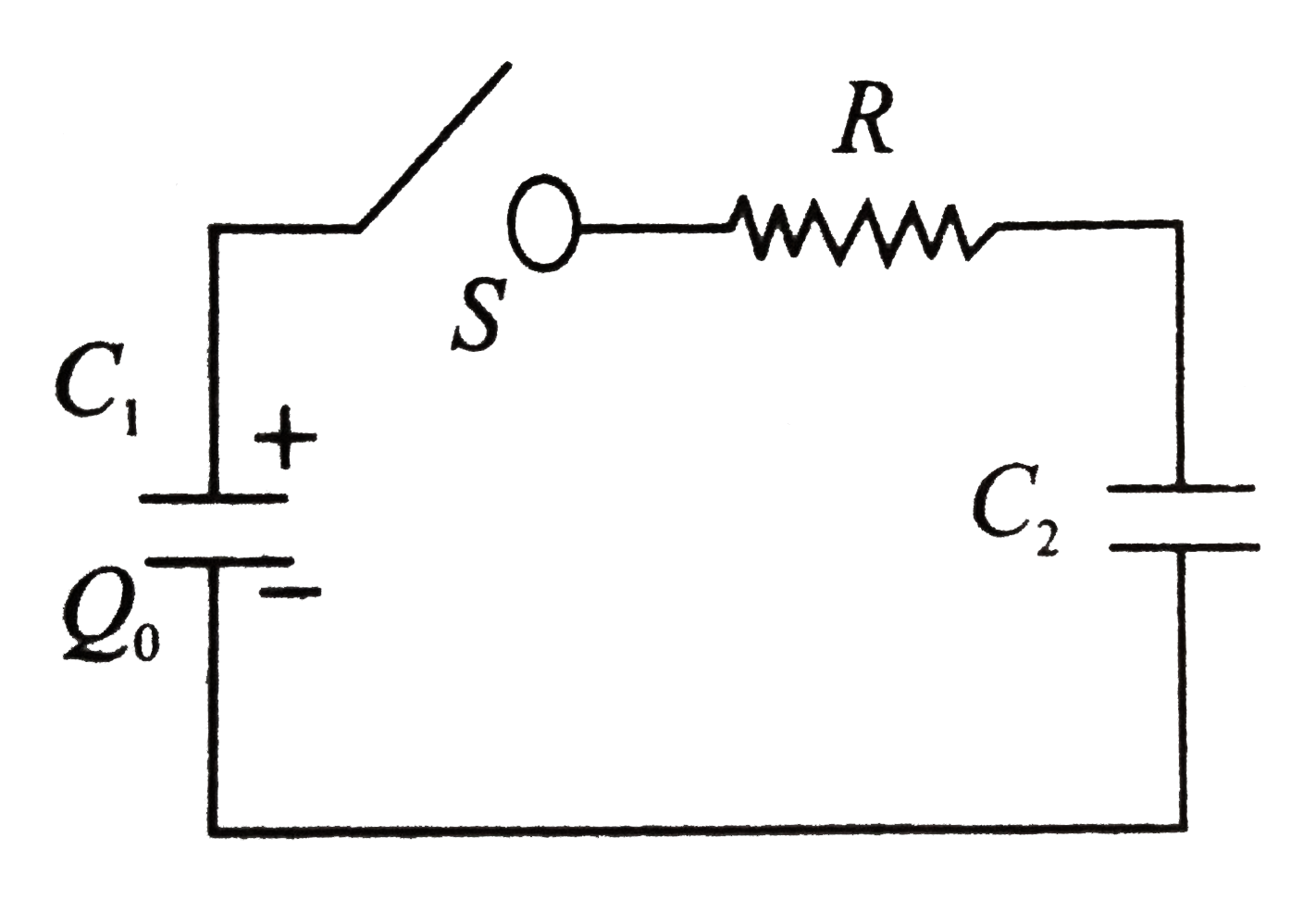
In the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
View SolutionInitially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionInitially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is

View SolutionThe switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
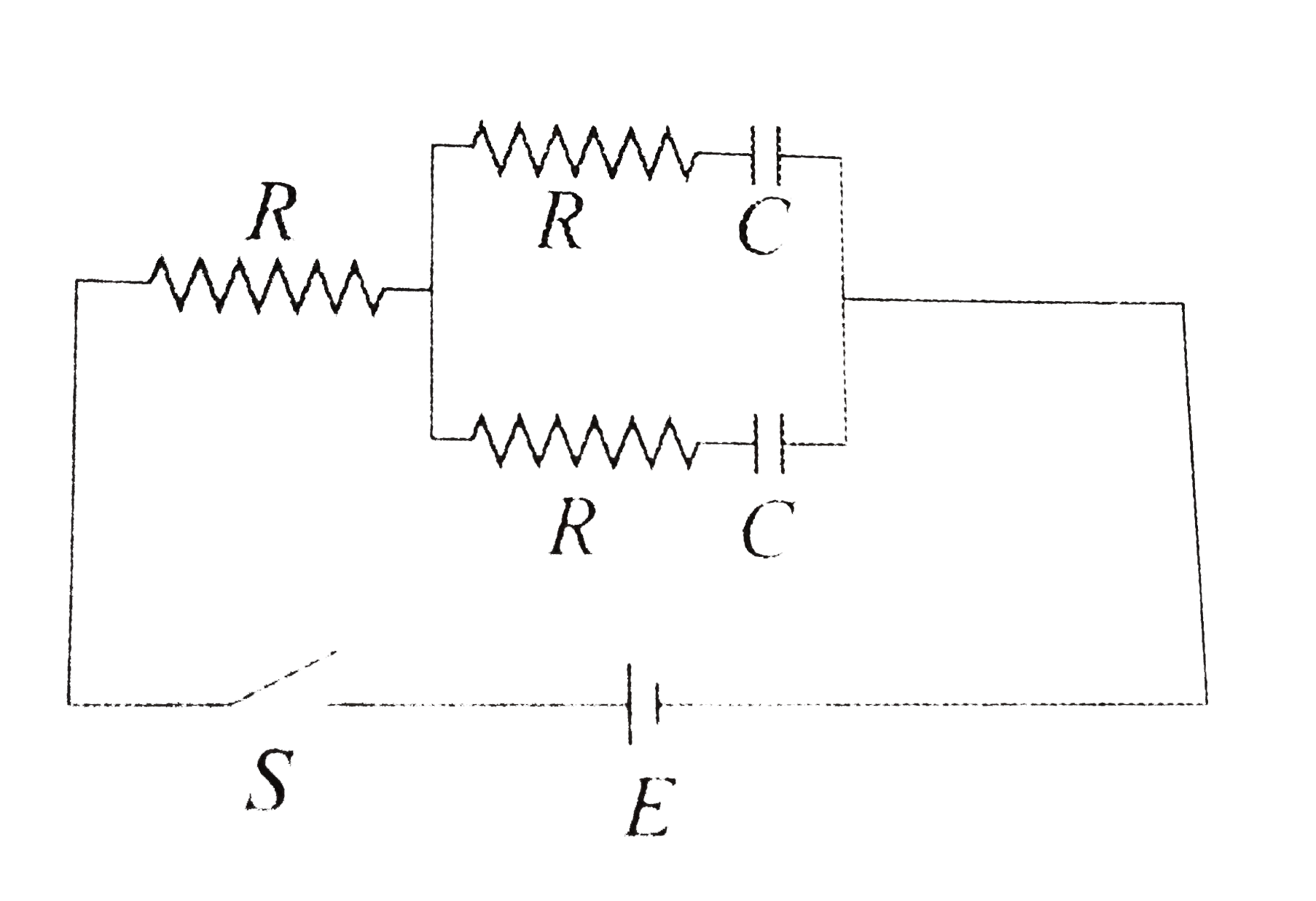
View Solution
