The correct relation between scattering angle (θ), impact parameter (b) and distance of closest approach (D) is
sinθ=Db
tanθ2=D2b
cosθb=D
cotθ2=b2D
The correct Answer is:B
To find the correct relation between the scattering angle (θ), impact parameter (b), and distance of closest approach (D), we can follow these steps:
Step 1: Understand the Concept of Distance of Closest Approach
The distance of closest approach (D) is defined as the minimum distance between the alpha particle and the nucleus when the alpha particle is deflected due to the electrostatic force. At this point, the kinetic energy of the alpha particle is equal to the potential energy due to the electrostatic interaction with the nucleus.
Step 2: Set Up the Energy Relation
The kinetic energy (KE) of the alpha particle can be expressed as:
KE=12mv2
where m is the mass of the alpha particle and v is its velocity.
The potential energy (PE) at the distance of closest approach can be expressed using Coulomb's law:
PE=k⋅Z1Z2e2D
where k is Coulomb's constant, Z1 and Z2 are the atomic numbers of the interacting particles, and e is the charge of an electron.
Step 3: Equate Kinetic and Potential Energy
At the distance of closest approach, we set the kinetic energy equal to the potential energy:
12mv2=k⋅Z1Z2e2D
Step 4: Define the Impact Parameter
The impact parameter (b) is the perpendicular distance from the center of the nucleus to the line along which the alpha particle would travel if it were not deflected.
Step 5: Relate Scattering Angle to Impact Parameter
The scattering angle (θ) is related to the impact parameter and the distance of closest approach. The relationship can be derived from the geometry of the scattering process. The relationship is given by:
tan(θ2)=Db
Step 6: Derive the Final Relation
From the above relationship, we can rearrange it to express D in terms of b and θ:
D=btan(θ2)
Step 7: Final Relation
Using the small angle approximation for tan(θ2)≈θ2 when θ is small, we can express the relationship as:
D≈b⋅θ2
This can be rearranged to give:
θ2=Db
Conclusion
Thus, the correct relation between the scattering angle (θ), impact parameter (b), and distance of closest approach (D) is:
θ2=Db
The distance of closest approach (D) is defined as the minimum distance between the alpha particle and the nucleus when the alpha particle is deflected due to the electrostatic force. At this point, the kinetic energy of the alpha particle is equal to the potential energy due to the electrostatic interaction with the nucleus.
The kinetic energy (KE) of the alpha particle can be expressed as:
KE=12mv2
where m is the mass of the alpha particle and v is its velocity.
PE=k⋅Z1Z2e2D
where k is Coulomb's constant, Z1 and Z2 are the atomic numbers of the interacting particles, and e is the charge of an electron.
At the distance of closest approach, we set the kinetic energy equal to the potential energy:
12mv2=k⋅Z1Z2e2D
The impact parameter (b) is the perpendicular distance from the center of the nucleus to the line along which the alpha particle would travel if it were not deflected.
The scattering angle (θ) is related to the impact parameter and the distance of closest approach. The relationship can be derived from the geometry of the scattering process. The relationship is given by:
tan(θ2)=Db
From the above relationship, we can rearrange it to express D in terms of b and θ:
D=btan(θ2)
Using the small angle approximation for tan(θ2)≈θ2 when θ is small, we can express the relationship as:
D≈b⋅θ2
This can be rearranged to give:
θ2=Db
Thus, the correct relation between the scattering angle (θ), impact parameter (b), and distance of closest approach (D) is:
θ2=Db
Topper's Solved these Questions
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
- ALTERNATING CURRENT BOOK - DISHA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Exercise -2 : Concept Applicator
30 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 29 : (COMMUNICATION SYSTEMS)
15 Videos
Similar Questions
Knowledge Check
In α- ray scattering, the scattering angle (θ) for impact parameter (b) to become zero is
A0∘B90∘C180∘D45∘.An α− paticle approaches the target nucleus of copper (Z = 29) is such a way that the vlaue of impact parameter is zero. The distance of closest approach will be
A2πε0(K.E.)α29e2B29e22πε0(K.E.)αC4πε0(K.E.)α29e2D(K.E.)α
Write the relation between kinetic energy of α- particle and its distance of closest approach from nucleus in Rutherford α-scattering experiment.
View SolutionWhat happens to the kinetic energy of the particle at the distance of closest approach?
View SolutionWrite the relation for (i) the distance of closest approach and (ii) impact parameter.
View SolutionWrite the relation for (i) the distance of closest approach and (ii) impact parameter.
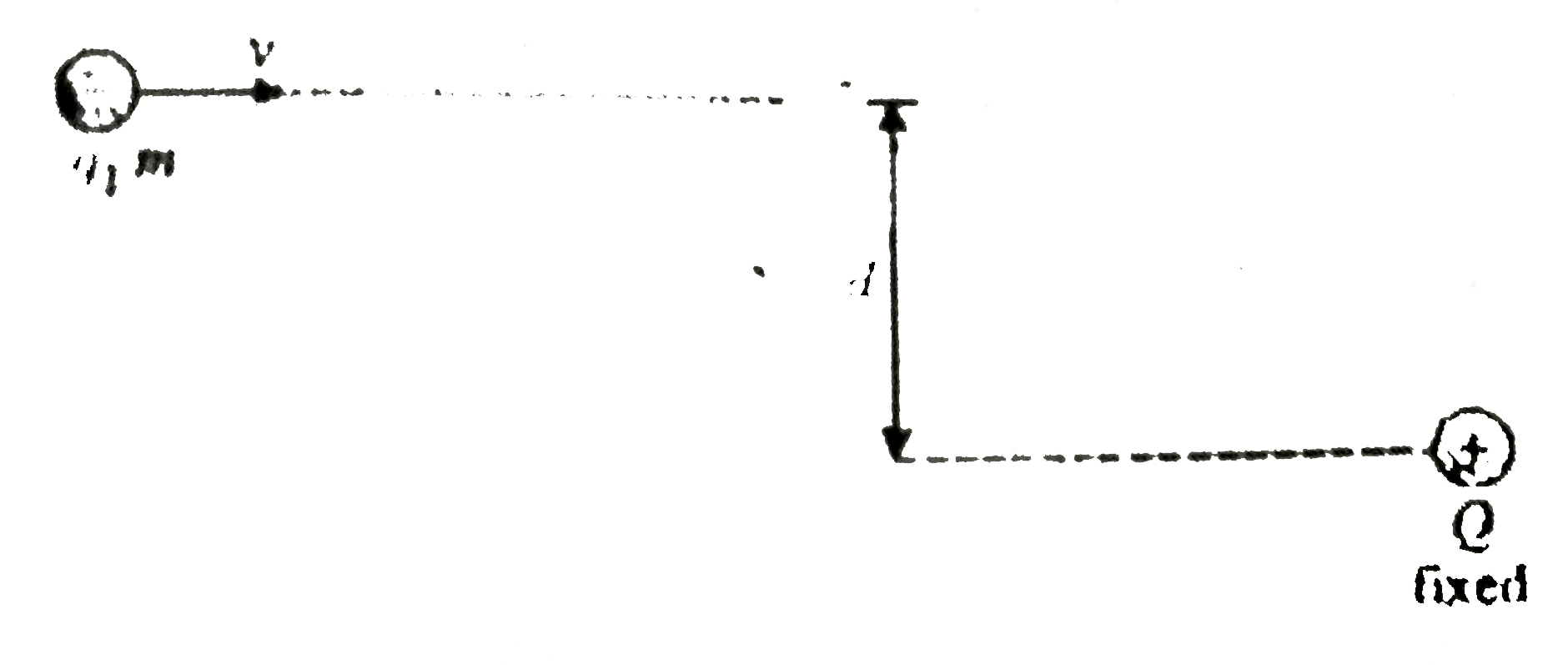
View SolutionFigure shows a charge +Q clamped at a point in free space. From a large distance another charge particle of charge -q an.d mass m is thrown toward +Q with an impact parameter d as shown with speed v. Find the distance of closest approach of the two particles.
View SolutionThe angle of scattering for zero value of impact parameter 'b' is________.
View Solution
