100 coplanar forces each equal to 10 n act on a body. Each force makes angle π/50 with the preceding force. What is the resultant of the forces.
1000 N
500 N
250 N
Zero
The correct Answer is:D
To find the resultant of 100 coplanar forces, each of 10 N, acting at an angle of π50 radians with respect to the preceding force, we can use the concept of vector addition.
1. Identify the Forces:
Each force F is given as 10 N, and there are 100 such forces.
2. Determine the Angle Between Forces:
The angle between each consecutive force is θ=π50 radians.
3. Calculate the Resultant Force:
The forces can be represented as vectors in a plane. The resultant R of these forces can be calculated using the formula for the resultant of forces acting at an angle:
R=n⋅F⋅cos((n−1)θ2)
where n is the number of forces, F is the magnitude of each force, and θ is the angle between the forces.
4. Substituting Values:
Here, n=100, F=10N, and θ=π50:
R=100⋅10⋅cos((100−1)⋅π502)
Simplifying the angle:
R=1000⋅cos(99⋅π502)
R=1000⋅cos(99π100)
5. Calculate the Cosine:
The cosine of 99π100 can be calculated:
cos(99π100)=−cos(π100)
Thus:
R=1000⋅−cos(π100)
6. Final Result:
The resultant force R is negative, indicating that the resultant vector points in the opposite direction of the initial forces. The magnitude can be calculated using a calculator:
R≈1000⋅−0.99985≈−999.85N
Therefore, the magnitude of the resultant force is approximately 999.85N.
Final Answer:
The resultant of the 100 coplanar forces is approximately 999.85N in the direction opposite to the initial forces.
Each force F is given as 10 N, and there are 100 such forces.
The angle between each consecutive force is θ=π50 radians.
The forces can be represented as vectors in a plane. The resultant R of these forces can be calculated using the formula for the resultant of forces acting at an angle:
R=n⋅F⋅cos((n−1)θ2)
where n is the number of forces, F is the magnitude of each force, and θ is the angle between the forces.
Here, n=100, F=10N, and θ=π50:
R=100⋅10⋅cos((100−1)⋅π502)
Simplifying the angle:
R=1000⋅cos(99⋅π502)
R=1000⋅cos(99π100)
The cosine of 99π100 can be calculated:
cos(99π100)=−cos(π100)
Thus:
R=1000⋅−cos(π100)
The resultant force R is negative, indicating that the resultant vector points in the opposite direction of the initial forces. The magnitude can be calculated using a calculator:
R≈1000⋅−0.99985≈−999.85N
Therefore, the magnitude of the resultant force is approximately 999.85N.
The resultant of the 100 coplanar forces is approximately 999.85N in the direction opposite to the initial forces.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Units, Dimensions & Measurements)33videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (KINEMATICS)59videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Co-ordinate & Algebra)39videos
RACE
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
Similar Questions
12 forces each equal to P act on a body. reach force make angle of 30 with the next one, the resultant of all the forces is ?
View SolutionWe have n coplanar forces, each of magnitude T. If each force makes an angle 2πn with the preceding force, then the vector sum of the n forces is a null vector.
View Solution
Knowledge Check
- Question 1 - Select One
Eleven forces each equal to 5N act on a particle simultaneously.If each force makes an angle 30∘ with the next one, the resultant of all forces is
A15NB55NC5NDzero - Question 2 - Select One
Five equal forces each of 20N are acting at a point in the same plane. If the angles between them are same, the resultant of these forces is
A0B40NC20ND20√2N - Question 3 - Select One
Two forces, each equal to F, act as shown in figure. Their resultant is
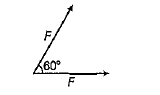 AF/2BFC√3D√5F
AF/2BFC√3D√5F
Find the vector sum of N coplanar forces, each of the magnitude F,when each force makes an angle of 2π/N with that preceding it.
View SolutionFind the vector sum of N coplanar forces, each of the magnitude F,when each force makes an angle of 2π/N with that preceding it.
View SolutionTwo forces, each equal to F, act as shown in (figure) Their resultant is
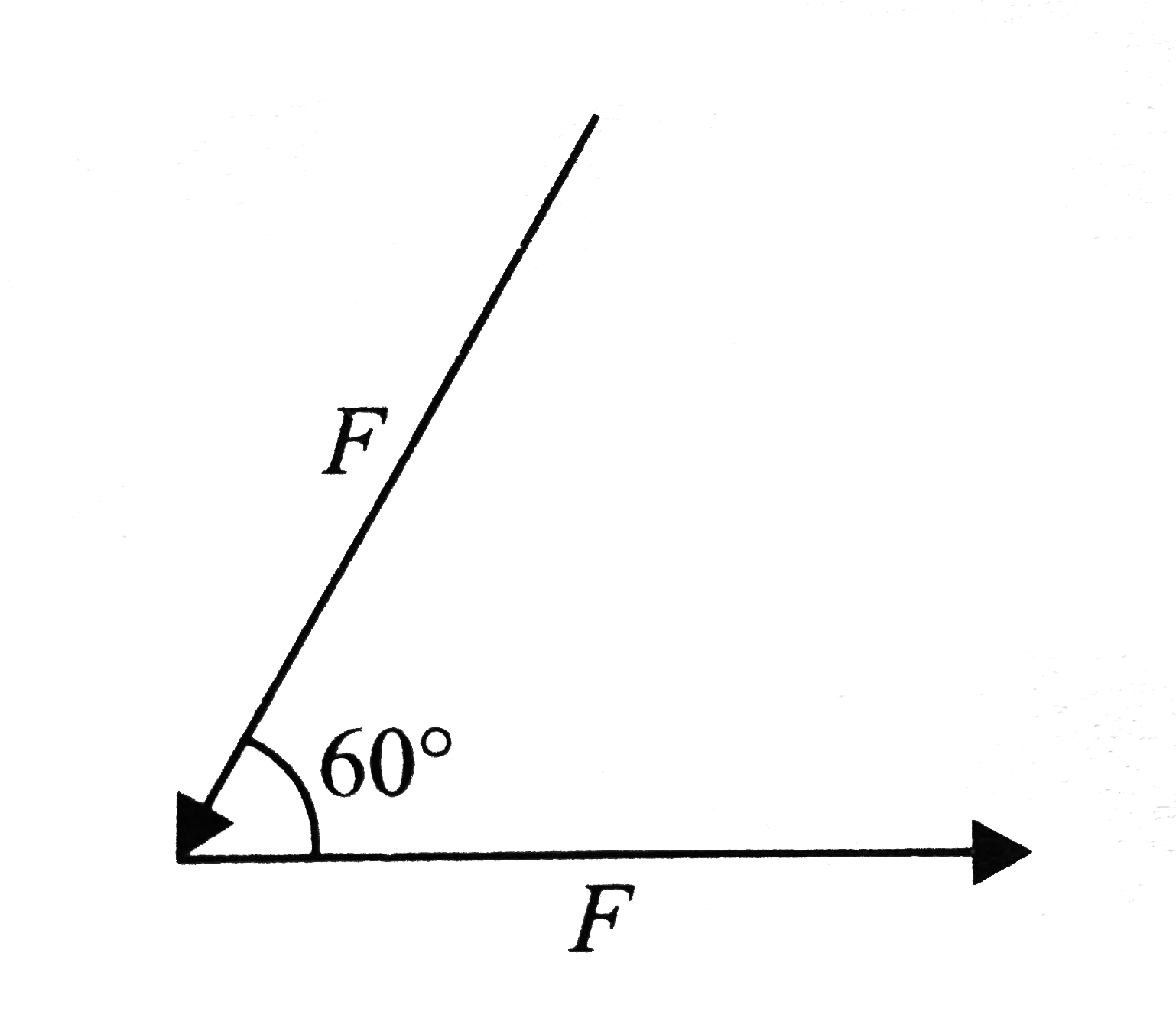 View Solution
View SolutionTwo forces, with equal magnitude F, act on a body and the magnitude of the resultant force is F3. The angle between the two forces is:
View SolutionTwo forces 10 N and 15 N are acting on a body then which cannot be the resultant of these two forces
View Solution

