A particle moves in a circle of radius 1 m with speed of 1 m/s. After completing half cycle. Find out :-
(i) Displacement
(ii) Distance travelled
(iii) Average velocity
(iv) Average acceleration
The correct Answer is:(i) 2m,
(ii) πm
(iii)2π
(iv) 2πm/s2
To solve the problem step by step, we will analyze the motion of a particle moving in a circle of radius 1 meter with a speed of 1 m/s after completing half a cycle.
Step 1: Calculate the Distance Travelled
The particle moves in a circular path. The distance travelled by the particle after completing half a cycle (which is half the circumference of the circle) can be calculated using the formula for the circumference of a circle:
Circumference=2πr
For a radius r=1 m:
Circumference=2π×1=2πm
Since the particle completes half a cycle, the distance travelled is:
Distance travelled=12×2π=πm
Step 2: Calculate the Displacement
Displacement is defined as the shortest distance between the initial and final positions of the particle. After completing half a cycle, the particle moves from one point on the circle to the point directly opposite it.
Since the radius of the circle is 1 m, the displacement can be calculated as the diameter of the circle:
Displacement=2r=2×1=2m
Step 3: Calculate the Average Velocity
Average velocity is defined as the total displacement divided by the total time taken.
We already calculated:
- Displacement = 2 m
Now, we need to calculate the time taken to complete half a cycle. The time taken t can be calculated using the formula:
t=Distance travelledSpeed
Substituting the values:
t=π1=πs
Now, we can calculate the average velocity:
Average Velocity=DisplacementTime=2mπs
Step 4: Calculate the Average Acceleration
Average acceleration is defined as the change in velocity divided by the time taken.
The initial velocity →vi is directed tangentially at the starting point, and the final velocity →vf is directed tangentially at the opposite point. Since these velocities are in opposite directions, we can consider their magnitudes:
Change in velocity=|→vf−→vi|=|(−1)−(1)|=2m/s
Now, we can calculate the average acceleration:
Average Acceleration=Change in velocityTime=2m/sπs=2πm/s2
Summary of Results
1. Displacement: 2 m
2. Distance travelled: π m
3. Average velocity: 2πm/s
4. Average acceleration: 2πm/s2
The particle moves in a circular path. The distance travelled by the particle after completing half a cycle (which is half the circumference of the circle) can be calculated using the formula for the circumference of a circle:
Displacement is defined as the shortest distance between the initial and final positions of the particle. After completing half a cycle, the particle moves from one point on the circle to the point directly opposite it.
Average velocity is defined as the total displacement divided by the total time taken.
- Displacement = 2 m
Average acceleration is defined as the change in velocity divided by the time taken.
1. Displacement: 2 m
2. Distance travelled: π m
3. Average velocity: 2πm/s
4. Average acceleration: 2πm/s2
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (NEWTONS LAWS OF MOTION)44videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (FRICTION)11videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Units, Dimensions & Measurements)33videos
RACE
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
Similar Questions
A particle moves in a circle of radius 4m with a linear speed of 20m/s. Find the angular speed.
View SolutionA particle is moving with constant speed v on a circular path of 'r' radius when it has moved by angle 60∘, Find
(i) Displacement of particle
(ii) Average velocity
(iii) Average accelerationView Solution
Knowledge Check
- Question 1 - Select One
A particle moves in a circle of radius 20 cm with linear speed of 10 m/s. Find the angular velocity
A500radsB150radsC50radsD15rads - Question 2 - Select One
A particle is moving in a circle of radius 4cm with constant speed of 1cm/s. Find
(a) time period of the particle.
(b) average speed, average velocity and average acceleration in a time interval from t=0 to t=T4. Here, T is the time period of the particle. Give only their magnitudes.AT=2s , 1.9cm/s 0.23cm/s2BT=25.13s , 0.9cm/s 2.23cm/s2CT=15.13s , 1.9cm/s 1.23cm/s2DT=25.13s , 0.9cm/s 0.23cm/s2 - Question 3 - Select One
A particle is moving along a circle of radius 1 m at a speed of 2 m/s .If the speed is incresed at the rate of 3 m/s2 then the resultant acceleration is
A2m/s2B3m/s2C5m/s2D10m/s2
A particle moves in a circle of radius R=2122m with constant speed 1m/s. Find,
(a) magnitude of average velocity and
(b) magnitude of average acceleration in 2 s.View SolutionA cyclist moving an a circular track of radius 50m completes one revolution in 2minutes. What is his (i) distance covered (ii) dislacement (iii) average speed (iv) average velocity, in one full revolution.
View SolutionFigure shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5 m at a given instant of time. At this instant, Find: (i) the radial acceleration, (ii) the speed of the particle and (iii) its tangential acceleration.
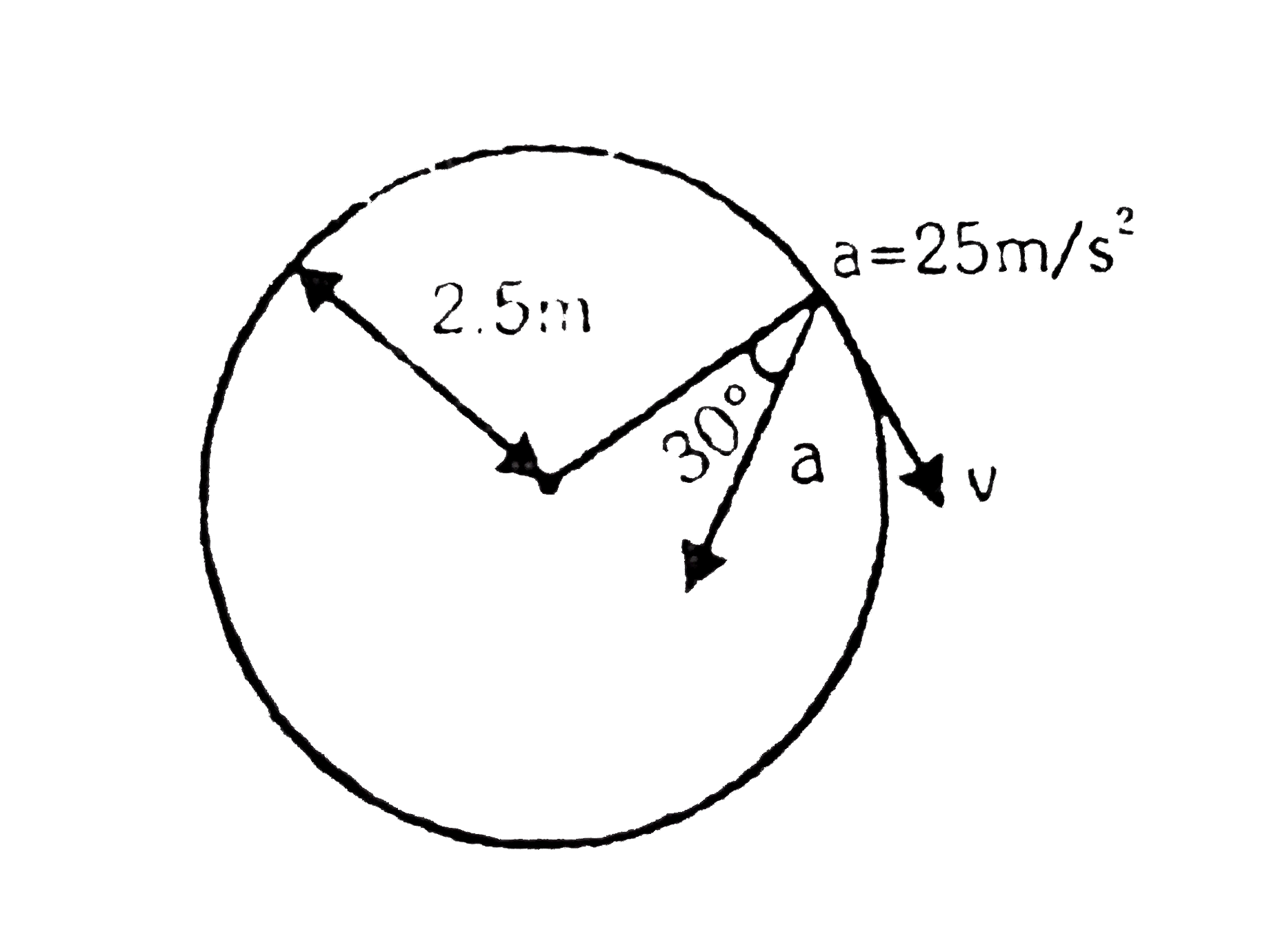 View Solution
View SolutionA particle comes round a circle of radius 1 m once. The time taken by it is 10 sec . The average velocity of motion is
View SolutionA particle of mass m moves in a circle of radius R with a uniform speed v.
(i) the angular speed of particle is v/R.
(ii) the time period of revolution is 2πR/v.
(iii) the acceleration of particle is v2/R.
(iv) the work done by the centripetal force in half revolution is (mv2/R)×πR.View Solution

