The medians CD and BE of an equilateral triangle ABC intersect each other at O. The ratio of $Δ O D E : Δ A B C$

Video Solution

|

Answer

Step by step video & image solution for The medians CD and BE of an equilateral triangle ABC intersect each other at O. The ratio of DeltaODE:DeltaABC by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Similar Questions

The medians CD and BE of an equilateral triangle ABC intersect each other at O. The ratio of $Δ O D E : Δ A B C$
View Solution
The medians $C D$ and $B E$ of an equilateral triangle $A B C$ intersect each other at $O .$ The ratio of $Δ O D E :$ $Δ A B C$ is equal to
View Solution

Knowledge Check

Question 1 - Select One
ABC is a triangle median CD and BE intersects at point O then find the ratio of area $(Δ O D E) : (Δ A B C)$ .
A $12 : 1$
B $4 : 3$
C $3 : 4$
D $1 : 12$
Question 2 - Select One
If the medians of two equilateral triangles are in the ratio 3:2, then what is ratio of the sides?
A $1 : 1$
B $2 : 3$
C $3 : 2$
D $\sqrt{3} : \sqrt{2}$
Question 3 - Select One
In given $Δ A B C$ , AD and BE are medians of triangle which intersect each other at point G. If area of $Δ B D G$ is 1 $c m^{2}$ , then what is the area of DCEG?

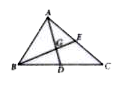A2 $c m^{2}$
B $3 c m^{2}$
C $4 c m^{2}$
D $1 c m^{2}$

Recommended Questions

Home
Ask Doubt
Profile