A rigid massless rod of length has two masses attached at each end as shown in the figure. The rod is pivoted at point P on the horizontal axis (see figuare). When released from initial horizontal position, its instantaneous angular acceleration will be

Step by step video & image solution for A rigid massless rod of length 3l has two masses attached at each end as shown in the figure. The rod is pivoted at point P on the horizontal axis (see figuare). When released from initial horizontal position, its instantaneous angular acceleration will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A uniform rod of length l and mass M pivoted about its end as shown in Fig. and is free to rotate in the vertical plane about the pivot. The rod is released from rest in the horizontal position.
(a) What is the initial angular acceleration of the rod?

(b) Find the initial acceleration of the right end of the rod?
( c) Find normal contact force due to hinge when rod has rotated through angle θ as shown in Fig.
View SolutionA uniform thin rod is released from rest in the horizontal position as shown in the figure. For what value of x, the angular acceleration is maximum.
View Solution
Knowledge Check
A uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?A47B57mgC137mgD117mgTwo blocks each of the mass m are attached to the ends of a massless rod which pivots as shown in figure. Initially the rod is held in the horizontal position and then released. Calculate the initial angular acceleration.
 A(l2−l1)gl21+l22 clockwiseB(l2+l1)g(l22+l21) clockwiseC(l2−l1)g2(l22+l21) clockwiseDgl2+l1 clockwise
A(l2−l1)gl21+l22 clockwiseB(l2+l1)g(l22+l21) clockwiseC(l2−l1)g2(l22+l21) clockwiseDgl2+l1 clockwiseA massless rod S having length 2l has equal point masses attached to its two ends as shown in figure. The rod is rotating about an axis passing through its centre and making angle α with the axis. The magnitude of change of momentum of rod i.e., ∣∣∣dLdt∣∣∣ equals
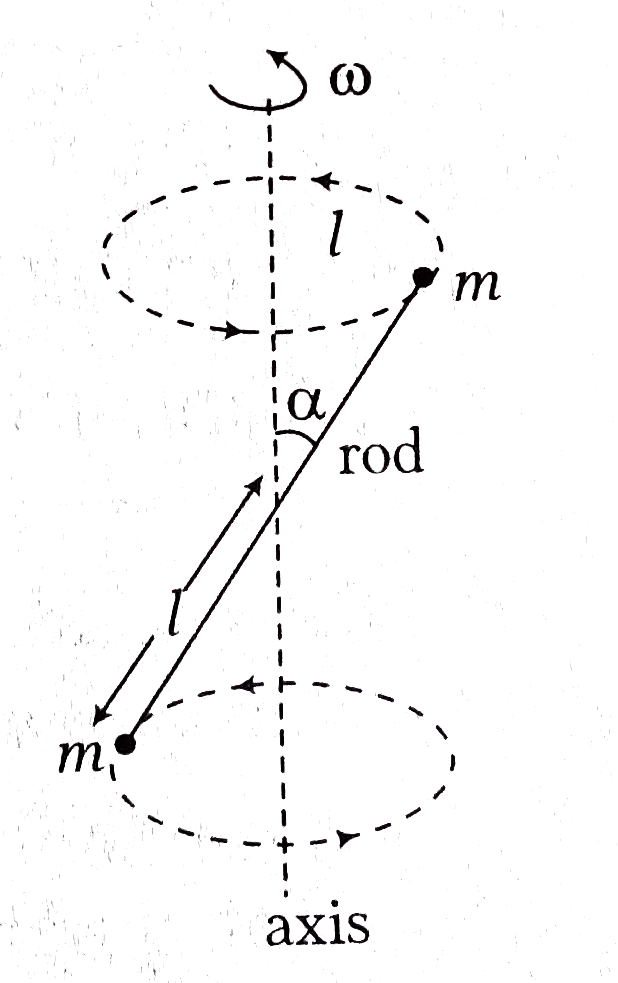 A2ml3ω2sinθ.cosθBml2ω2sin2θCml2sin2θDm1/2l1/2ωsinθ.Cosθ
A2ml3ω2sinθ.cosθBml2ω2sin2θCml2sin2θDm1/2l1/2ωsinθ.Cosθ
A light rigid rod of length 4m is connected rigidly with two identical particles each of mass m=2kg. the free end of the rod is smoothly pivoted at O. The rod is released from rest from its horizontal position at t=0. Find the
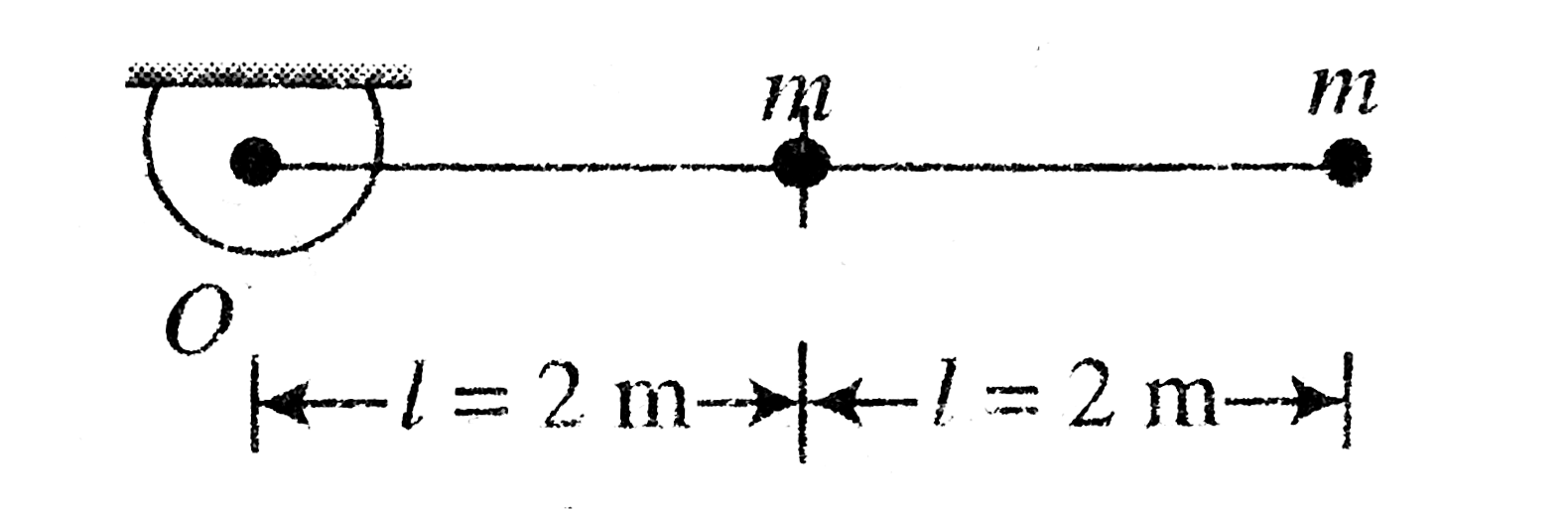
reaction offered by the pivot at t=0 (in N).
View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml2/3, the initial angular acceleration of the rod will be
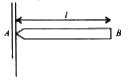
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be
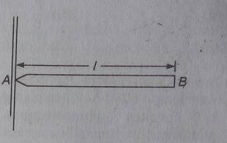
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be

View Solution
