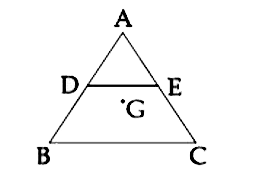
An equilateral triangle ABC is cut from a thin solid sheet of wood .(see figure ) D,E and F are the mid-points of its sides as shown and G is the centre of the triangle.The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane to the triangle is I0 If the smaller triangle DEF is removed from ABC , the moment of inertia of the remaining figure about the same axis is I. Then :
An equilateral triangle ABC is cut from a thin solid sheet of wood .(see figure ) D,E and F are the mid-points of its sides as shown and G is the centre of the triangle.The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane to the triangle is I(0) If the smaller triangle DEF is removed from ABC , the moment of inertia of the remaining figure about the same axis is I. Then :

A

I=1516I0

B

I=34I0

C

I=916I0

D

I=I04

Video Solution
Doubtnut Promotions Banner
|
Answer

Step by step video & image solution for An equilateral triangle ABC is cut from a thin solid sheet of wood .(see figure ) D,E and F are the mid-points of its sides as shown and G is the centre of the triangle.The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane to the triangle is I_(0) If the smaller triangle DEF is removed from ABC , the moment of inertia of the remaining figure about the same axis is I. Then : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12PHYSICSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • D,E and F are the middle points of the sides of the triangle ABC, then

    Acentroid of the triangle DEF is the same as that of ABC
    Borthocentre of the traiangl DRF is the circumcentre of ABC
    Corthocentre of the triangle DEF is the incentre of ABC
    Dcentroid of the triangle DEF is not the same as that of ABC

  • Three point masses each of mass m are placed at the corners of an equilateral triangle of side 'a'. Then the moment of inertia of this system about an axis passing along one side of the triangle is

    Ama2
    B3ma2
    C34ma2
    D23ma2

  • Three particles each of 'm' are kept at the three vertices of an equilateral triangle of side 'a' . Moment of inertia of the system about an axis passing through the centroid and perpendicular to its plane is

    A3ma2
    Bma2
    Cma2/3
    D2/3ma2