A concave mirror used for face viewing has focal length of 0.4m. The distance at which you hold the mirror from your face in order to see your image upright with a magnification of 5 is ______ (in m).
0.24m
1.60 m
0.32 m
0.16 m
The correct Answer is:c
+5=−vu⇒v=−5u
Using 1v+1u=1f⇒1−5u+1u=−10.4
∴U=−0.32m
Topper's Solved these Questions
Similar Questions
A convex mirror used on a bus has a focal length of 200 cm. If a scooter is located at 100 cm. from this mirror find the position, nature and magnification of the image formed in the mirror.
View SolutionA concave mirror has a focal length of 5 cm. When an object is placed at a distance of 15 cm from the mirror, then the image is formed in front of the mirror at ____cm.
View Solution
Knowledge Check
- Question 1 - Select One
A concave mirror of focal length f produces a real image n times the size of the object. The distance of the object from the mirror is
A(n−1)fB(n+1)fCn+1nfDn−1nf - Question 2 - Select One or More
For a concave mirror of focal length f, image is 2 times larger. Then the object distance from the mirror can be
Af2B3f2Cf4D4f3 - Question 3 - Select One
An object is moving away from concave mirror of focal length f starting from focus. The distance of an object from pole of mirror is x. The correct graph of magnitude of magnification(m) verses distance x is:
A B
B C
C D
D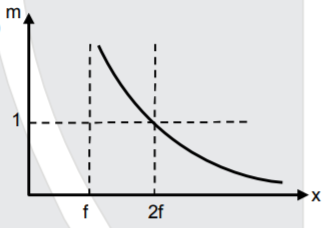
A convex mirror used for rear view on an automobile has a radius of curvature of 3.00 m. If a bus is located at 5.00 m from this mirror, find the position, nature and magnification of the image.
View SolutionState one way in which your mirror image differs from you.
View SolutionA concave mirror of focal lengthfproduces a real imagentime the size of the object.What is the distance of the object from the mirror.
View SolutionThe distance of real object when a concave mirror produces a real image of magnification ‘m’ is (f is focal length)
View SolutionA concave mirror has focal length 15cm. If an object is placed at a distance of 30 cm from the mirror, then image formed by the mirror lies at a distance (from the mirror)
View Solution

