When the sun appears to be just on horizon, it is in fact below the horizon. This is because the light from the sun bends when it enters the earth’s atmosphere. Let us assume that atmosphere is uniform and has index of refraction equal to $μ$ . It extends upto a height $h (< < R =$ radius of earth) above the earth’s surface. In absence of atmosphere how late would we see the sunrise compared to what we see now? Take time period of rotation of earth to be T. Calculate this time for following data
$R = 6400 k m, μ = 1.0003, h = 20 k m, T = 24 h r$ .

Video Solution

Text Solution

Verified by Experts

Just as the Sun disappears, your line of sight to the top of the Sun is tangent to Earth.s surface at point A while lying and point B while standing as shown in Fig Your eyes are located at point A while you are lying, and at height h above point A while you are standing.
Let d represent the distance between point B and the location of your eyes when you are standing, and r the radius of Earth. From Pythagorean theorem, we have
$d^{2} + r^{2} = {(r + h)}^{2} = r^{2} + 2 r h + h^{2}$
$d^{2} = 2 r h + h^{2} (1 - 7)$
Because the height h is so much smaller than Earth.s radius r, the term $h^{2}$ is negligible compared to the term 2rh, and we can rewrite Eq. 1-7 as
$d^{2} = 2 r h (1 - 8)$
In Fig. 1-2, the angle between the radii to the two-tangent points A and B is $θ$ , which is also the angle through which the Sun moves about Earth during the measured time $t = 11.1 s$ . During a full day, which is approximately 24 h, the Sun moves through an angle of $360^{\circ}$ about Earth. Thus, we can write
$\frac{θ}{360^{\circ}} = \frac{t}{24 h}$
$t = 11.1 s$ gives us
$θ = \frac{(360^{\circ}) (11.1 s)}{(24 h) (60 min / h) (60 s / min)} = {0.04625}^{\circ}$ .
In Fig. 1-2, we see that $d = r tan θ$ . Substituting this for d in Eq. 1-8 gives us
$r^{2} {tan}^{2} θ = 2 r h$
$r = \frac{2 h}{{tan}^{2}} θ$
Substituting $θ = {0.04625}^{\circ} and h = 1.70 m$ , we find
$r = \frac{(2) (1.70 m)}{{tan}^{2} {0.04625}^{\circ}} = 5.22 \times 10^{6} m$
This radius is within 20% of the accepted value $(6.37 \times 10^{6} m)$ for the (mean) radius of Earth.

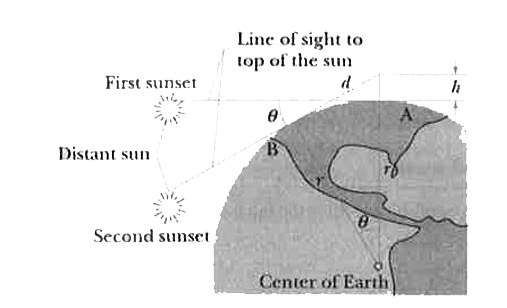
Fig 1-2 Your line of sight to the top of the setting Sun rotates through the angle $θ$ when you stand up at point A and elevate your eyes by a distance h. (Angle $θ$ and distanc h are exaggerated here for clarity).

Updated on:21/07/2023

When the sun is either rising or setting and appears to be just in the horizon, it is in fact below the horizon. The explanation for this seeming paradox is that light from the sun bends slightly when entering the earth's atmosphere as shown in figure. Assume that the atmosphere has uniform density and hence uniform index of refraction n and extends to a height h above the earth's surface, at which point is abruptly stop. The angle $δ$ above the Sun's true position is given by

A ${sin}^{- 1} (\frac{n R}{R + h})$
B ${sin}^{- 1} (\frac{R}{R + h})$
C ${sin}^{- 1} (\frac{n R}{R + h}) + {sin}^{- 1} (\frac{R}{R + h})$
D ${sin}^{- 1} (\frac{n R}{R + h}) - {sin}^{- 1} (\frac{R}{R + h})$
The earth binds the atmosphere because of
AGravity
BOxygen between earth and atrnosphere
CBoth (a) and (b)
DNone
We can see the Sun even when it is little below the horizon because of
AReflection of light
BRefraction of light
CDispersion of light
DAbsorption of light