Two skaters on frictionless ice hold opposite ends of a pole of negligible mass. An axis runs along it, with the origin at the center of mass of the two-skater system. One skater, Fred , weighs twice as much as the other skater, Ethel. Where do the skaters meet if (a) Fred pulls hand over along the pole so as to draw himself to Ethel , (b) Ethel pulls hand over hand to draw herself to Fred, and (c ) both skaters pull hand over hand ?
The correct Answer is:(a)-(c) At the center of mass , still at the origin (their forces are internal to the system an cannot move the center of mass)
To solve the problem step by step, we need to analyze the situation involving the two skaters, Fred and Ethel, and their center of mass.
1. Identify the Masses:
- Let the mass of Ethel be m.
- Therefore, the mass of Fred, who weighs twice as much, will be 2m.
2. Determine the Center of Mass:
- The center of mass (CM) of the system can be calculated using the formula:
xCM=m1x1+m2x2m1+m2
- Assume Ethel is at position −d and Fred is at position d (with the origin at the center of mass):
xCM=(m)(−d)+(2m)(d)m+2m=−md+2md3m=md3m=d3
- Since the center of mass is at the origin, we have:
xCM=0
3. Analyze Each Scenario:
- (a) Fred pulls himself towards Ethel:
- As Fred pulls himself towards Ethel, he moves closer to the center of mass. The center of mass remains unchanged (at the origin), so they will meet at the center of mass, which is at x=0.
- (b) Ethel pulls herself towards Fred:
- Similarly, when Ethel pulls herself towards Fred, she also moves towards the center of mass. Again, they will meet at the center of mass, which is at x=0.
- (c) Both skaters pull hand over hand:
- If both skaters pull themselves towards each other, they will still meet at the center of mass. The center of mass does not change, so they will meet at x=0.
4. Conclusion:
- In all three scenarios, Fred and Ethel will meet at the center of mass, which is at the origin x=0.
Final Answer:
In all cases (a), (b), and (c), the skaters meet at the center of mass, which is at x=0.
- Let the mass of Ethel be m.
- Therefore, the mass of Fred, who weighs twice as much, will be 2m.
- The center of mass (CM) of the system can be calculated using the formula:
xCM=m1x1+m2x2m1+m2
- Assume Ethel is at position −d and Fred is at position d (with the origin at the center of mass):
xCM=(m)(−d)+(2m)(d)m+2m=−md+2md3m=md3m=d3
- Since the center of mass is at the origin, we have:
xCM=0
- (a) Fred pulls himself towards Ethel:
- As Fred pulls himself towards Ethel, he moves closer to the center of mass. The center of mass remains unchanged (at the origin), so they will meet at the center of mass, which is at x=0.
- Similarly, when Ethel pulls herself towards Fred, she also moves towards the center of mass. Again, they will meet at the center of mass, which is at x=0.
- If both skaters pull themselves towards each other, they will still meet at the center of mass. The center of mass does not change, so they will meet at x=0.
- In all three scenarios, Fred and Ethel will meet at the center of mass, which is at the origin x=0.
In all cases (a), (b), and (c), the skaters meet at the center of mass, which is at x=0.
Topper's Solved these Questions
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Problems
46 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Single Correct Choice )
47 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)
3 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)
3 Videos
Similar Questions
Draw the lines of force due to two bar magnets, north pole of one facing the south pole of the other.
View SolutionTwo skaters, one with mass 75 kg and the other with mass 40 kg, stand on an ice rink holding a pole of length 10 m and negligible mass. Starting from the ends of the pole. the skaters pull themselves along the pole until they meet. How far does the 40 kg skater move?
View SolutionIn Fig. 10-78, two skaters, each of mass 50 kg, approach each other along parallel paths separated by 3.0 m. They have opposite velocities of 1.4 m/s each. One skater carries one end of a long pole of negligible mass, and the other skater grabs the other end as she passes. The skaters then rotate around the center of the pole. Assume that the friction between skates and ice is negligible. What are (a)the radius of the circle, (b) the angular speed of the skaters, and ( c) the kinetic energy of the two skater system? Next, the skaters pull along the pole unyil they are separated by 1.0 m. What then are (d) their angular speed and (e) the kinetic energy of the system? (f) What provided the energy for the increased kinetic energy?

View SolutionA skater wearing his skates is oushing a wall. What will be the work done by the contact force on the skater as he moves away from the wall?
View SolutionShow the poles in the broken parts of the magnets when it is divided into two halves
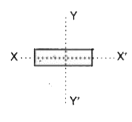
along the axis XX.
View SolutionShow the poles in the broken parts of the magnets when it is divided into two halves
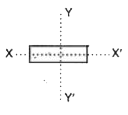
along the axis YY'.
View SolutionTwo particles of equal mass are moving along the same straight line with the same speed in opposite direction. What is the speed of the centre of mass of the system ?
View SolutionHow is a speed skater able to glide across the ice? How can the skater increase friction between the ice and the skates? What effect does an increase in friction have on the skater's speed ?
View SolutionDraw the lines of force due to two bar magnets, the north pole of one facing the north pole of the other.
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope , the force exerted by the rope on the block .
View Solution
