An aluminium cube of side 20cm floats in mercury. How much farther will the block sink when tempereture rises from 27∘C to 77∘C ? Density of aluminium and mercury at 27∘C are 2.7 and 13.6g/ while the coeficient of volume expansion of mercury and linear expansion of aluminium are 1.8×10−4/∘C and 23×10−6/∘C respectively.
KEY IDEA
As the temperature rises, the block expands and the density of the liquid decreases, so it like we are putting a bigger block of same weight in a lighter liquid . So , to apply the same buoyant force , a larger fraction of the volume should sink into the liquid .
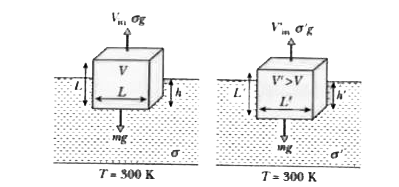
Calculations : If side of cube, density of liquid (mercury) and length of the floating cube inside the liquid are L.
σ,h, and L., σ.,h. at 300 K and 350 K , respectively , then by principle of floatation
m=Vinσ=V.inσ. (with m=Vρ=ρL3)
This is , as Vin=hA=hL2,
hL2σ=h.(L.)σ.
or [h.h]=[LL.]2×[σσ.]
Now as L. =L(1+α2ΔT)andσ.=σ(1+γLΔT) , therefore ,
[h.h]=(1+γLΔT)(1+αsΔT)=(1+γΔT)(1+2αsΔT)=1+(γL−2αs)ΔT
So, Δh,=(h.−h)=h(γL−2αs)×ΔT
Also, from the equation m=Vinσ, we have
ρL3=hL2σ
That is , h=[ρσ]L=[2.713.6]×20=3.970cm
So, Δh=3.970(1.8×10−4−2×23×10−6)(350−300)
=2.66×10−2cm
As expected the block sinks deeper.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - CHECKPOINT8videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PROBLEMS24videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)2videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PRACTICE QUESTIONS ( INTEGER TYPE )3videos
THE FIRST LAW OF THERMODYNAMICS
Similar Questions
The figure shows three temperature scales with the freezing and boiling points of water indicated.
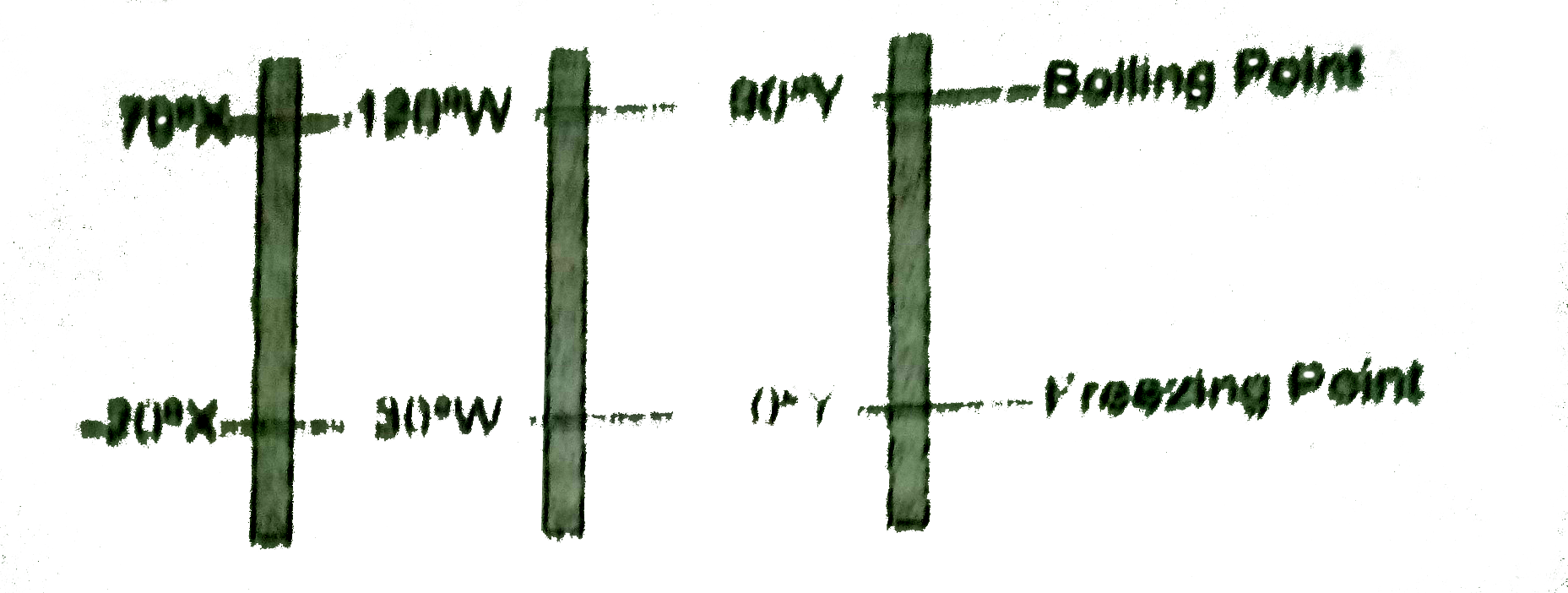
(a) Rank the size of a degree on these scales, greatest first.
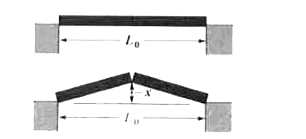
(b) Rank the following temperatures, highest first :50∘X,50∘W and 50∘Y.05:22View SolutionAs a result of a temperature rise of 64∘C , a bar with a crack at centre buckles upward (Fig . 18-20 ). The fixed distance L0 is 3.77 m and the coefficient of linear expansion of the bar is Find the rise 25×10−6/∘C of the centre .
 07:05View Solution
07:05View SolutionA uniform circular disc of mass 50kg and radius 0.4 m is rotating with an angular velocity of 10rads−1 about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m, are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (∈reds−1) of the system is
05:12View SolutionAn electric heater supplies heat to a system at a rate or 100 W. If the system performs work at a rate of 75 joules per second at what rate is the internal energy increasing ?
10:37View SolutionA wire is made by attaching two segments together end to end. One segment is made of aluminium and the other is steel. The effective coefficient of linear expansion of the two segment wire is 19xx10^(-6)//^(@)C . The fraction length of aluminium is (linear coefficient of thermal expansion of aluminium and steel are 23xx10^(-6).^(@)C and 12xx10^(-6)//^(@)C ,
03:55View SolutionA glass vessel is filled up to 3/5th of its volume by mercury. If the volume expansivities of glass and mercury be 9xx 10^(-6)//^(@)C and 18xx10^(-5)//^(@)C respectively, then the coefficient of apparent expansion of mercury is
01:51View SolutionA glass flask of volume one litre at 0∘C is filled level full of mercury at this temperature. The flask and mercury are now heating to 100∘C . How much mercury will spill out if coefficient of volume expansion of mercury is 1.2×10−4/∘C and linear expansion of glass is 1.0×10−4/∘C respectively ?
02:46View SolutionAn aluminium cube of side 20cm floats in mercury. How much farther will the block sink when tempereture rises from 27^(@)C to 77^(@)C ? Density of aluminium and mercury at 27^(@)C are 2.7 and 13.6g//cc while the coeficient of volume expansion of mercury and linear expansion of aluminium are 1.8xx10^(-4)//^(@)C and 23xx10^(-6)//^(@)C respectively.
View SolutionA glass vessel of volume 100cm3 is filled with mercury and is heated from 25∘C→75∘C. What volume of mercury will overflow? Coefficient of linear expansion of glass =1.8×10−6/'∘C and coefficeient of volume expansion of mercury is 1.8×10−4/'∘C.
03:06View SolutionCoefficient of volume expansion of mercury is 0.18×10−3/.∘C. If the density of mercury at 0∘C is 13.6g/cc, then its density at 200∘C is
03:50View SolutionDensity of mercury at 0∘C is 13.5955g⋅cm−3. If the coefficient of linear expansion of mercury is 0.000061∘C−1, find its density at 60∘C.
05:08View SolutionA piece of aluminium of relative density 2.7 floats in mercury. Find the fraction of volume of aluminium piece which remains outside the mercury. The density of mercury is 13.6 xx 10^3" kg/m"^(3).
05:33View SolutionA glass flask of volume 1 litre is fully filled with mercury at 0∘C. Both the flask and mercury are now heated to 100∘C. If the coefficient of volume expansion of mercury is 1.82×10−4/∘C, volume coefficient of linear expansion of glass is 10×10−6/∘C, the amount of mercury which overflows is
View SolutionA glass bulb of volume 250 c.c is completely filled with mercury at 20∘C. The temperature of the system is raised to 100∘C. If the coefficient of linear expansion of glass is 9×10−6/∘C and coefficient of absolute expansion of mercury is 1.8×10−4/∘C, the volume of mercury that overflows is nearly
01:51View SolutionA platinum sphere floats in mercury. Find the percentage change in the fraction of volume of sphere immersed in mercury when the temperature is raised by 80∘C (volume expansivity of mercury is 182×10−6/∘C and linear expansivity of platinum is 9×10−6/∘C respectively )
04:52View SolutionA platinum sphere floats in mercury. Find the percentage change in the fraction of volume of sphere immersed in mercury when the temperature is raised by 80°C: (volume expansivity of mercury is 182×10−6/°C and linear expansivity of platinum is 9×10−6/°C respectively )
06:05View Solution

