Question

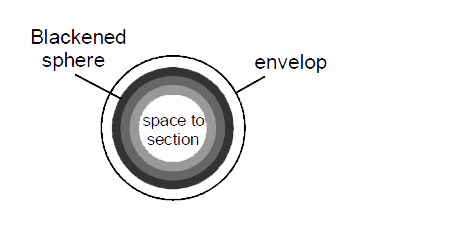
A space station is covered by an envelope which is a blackened shell. The temperature of the envelope is T = 500 K that is constant due to the operation of applicances of the station. Determine the temperature of the shell if the station is enveloped by a thin spherical black screen of nearly the same radius as the radius of the shell. Assume that there are no radiations on this space station.

Explanation

The total amount of heat Q emitted in space per unit time remains unchanged since it is determined by the energy liberated during the operation of the applicances of the station. As given in the question, the appliances produces heat at constant rate.
Since only the outer surface of the screen emits into space ( this radiation depends only on its temperature ), the temperature of the screen must be equal to the initial temperature T = 500K of the station. Also, it is important to remember that the screen emits the same amount of heat Q inward. This radiation the envelope of the station and is absorbed by it.
Calculations `:` Therefore, the total amount of heat supplied to the station per unit is the sum of th heat Q liberated during the operation of the appliances and the amount of heat Q absorbed by the inner surface of the screen, that is, equal to 2Q. According to the heat balance condition, the same amount of heat must be emitted,
`2Q = A sigma T_(x)^(4)`
and hence
`(Q)/( 2Q) = ( T^(4))/( T_(x)^(4))`
where `T_(x)` is the required temperature of the envelope of the station. Finally, we obtain
`T_(x) = root (4)(2T) -= 600K`
The temperature of the envelope has increased because to gain in thermal equilibrium it must emit more energy than before as it is receiving more energy than before.