A cylindrical copper rod of length 0.60m and cross-sectional area 6.0 cm2 is insulated along its side. The ends are held at a temperature difference of 100∘C by having one end in a water -ice mixture and the other in a mixture of boiling water and steam. At what reate (a) is energy conducted by the rod and (b) does the ice melt ?
The correct Answer is:(a) 40J /s; (b) 0.12g/s
To solve the problem step by step, we will first calculate the rate of energy conducted by the copper rod and then determine the rate at which the ice melts.
Given Data:
- Length of the copper rod, L=0.60m
- Cross-sectional area, A=6.0cm2=6.0×10−4m2
- Temperature difference, ΔT=100∘C
- Thermal conductivity of copper, k=401W/m⋅K
Part (a): Rate of Energy Conducted by the Rod
1. Use Fourier's Law of Heat Conduction:
P=k⋅A⋅(TH−TC)L
Where:
- P is the rate of heat transfer (W)
- k is the thermal conductivity (W/m·K)
- A is the cross-sectional area (m²)
- TH−TC is the temperature difference (K)
- L is the length of the rod (m)
2. Substitute the values into the formula:
P=401W/m⋅K⋅6.0×10−4m2⋅100K0.60m
3. Calculate the numerator:
401⋅6.0×10−4⋅100=24060W⋅m2
4. Calculate the rate of heat transfer:
P=240600.60=40100W
5. Convert to Joules per second:
P=40J/s
Part (b): Rate at which the Ice Melts
1. Use the formula for the rate of melting ice:
dmdt=PLf
Where:
- dmdt is the mass of ice melted per second (g/s)
- Lf is the latent heat of fusion of ice (approximately 333J/g)
2. Substitute the values:
dmdt=40J/s333J/g
3. Calculate the rate of melting:
dmdt≈0.12012g/s≈0.12g/s
Final Answers:
- (a) The rate of energy conducted by the rod is 40 J/s.
- (b) The rate at which the ice melts is 0.12 g/s.
- Length of the copper rod, L=0.60m
- Cross-sectional area, A=6.0cm2=6.0×10−4m2
- Temperature difference, ΔT=100∘C
- Thermal conductivity of copper, k=401W/m⋅K
P=k⋅A⋅(TH−TC)L
Where:
- P is the rate of heat transfer (W)
- k is the thermal conductivity (W/m·K)
- A is the cross-sectional area (m²)
- TH−TC is the temperature difference (K)
- L is the length of the rod (m)
P=401W/m⋅K⋅6.0×10−4m2⋅100K0.60m
401⋅6.0×10−4⋅100=24060W⋅m2
P=240600.60=40100W
P=40J/s
dmdt=PLf
Where:
- dmdt is the mass of ice melted per second (g/s)
- Lf is the latent heat of fusion of ice (approximately 333J/g)
dmdt=40J/s333J/g
dmdt≈0.12012g/s≈0.12g/s
- (a) The rate of energy conducted by the rod is 40 J/s.
- (b) The rate at which the ice melts is 0.12 g/s.
Topper's Solved these Questions
- HEAT-MEASUREMENT AND TRANSFERBOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS
60 Videos
- HEAT-MEASUREMENT AND TRANSFERBOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS(MORE THAN ONE CORRECT CHOICE TYPE )
8 Videos
- HEAT-MEASUREMENT AND TRANSFERBOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - CHECKPOINT 2
1 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
4 Videos
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)
6 Videos
Similar Questions
A rod of length1m having cross sections area 0.75m^(2), conducts heat at 6000J/sec.Then the temperature difference across the rod isK=200Wm^(-1)k^(-1)
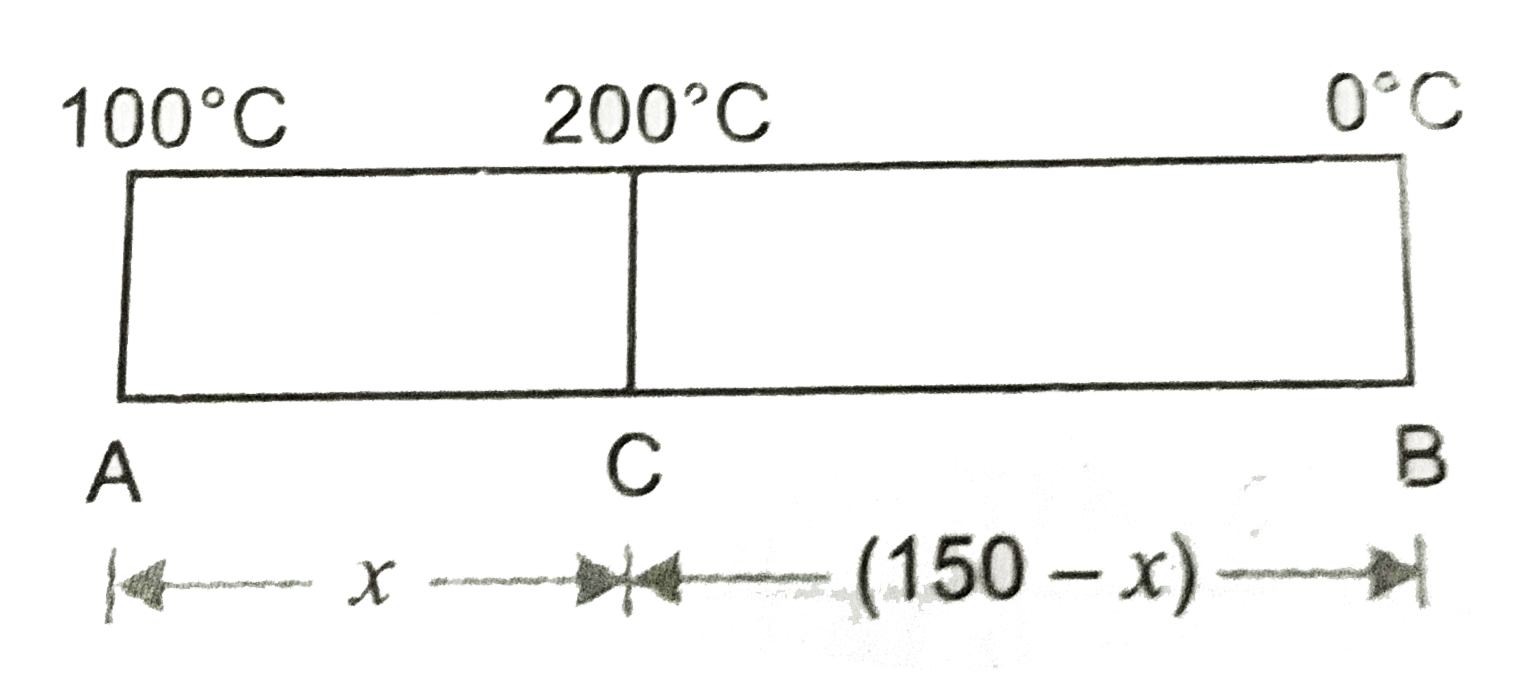
View SolutionOne end of a copper rod of uniform cross-section and length 150 cm is in contact with ice and the other end with water at 100∘C . At what point along its length should a temperature of 200∘C be maintained so that in steady state, the mass of the ice melting is equal to that of steam produced in the same interval of time? Assume that whole system is insulated from the surroundings. Latent heat of steam =537calg−1 and lalent heat of fusion of ice =80calg−1.
 .
.
View Solution
Knowledge Check
Cylinder rod of copper of length 2m and cross-sectional area 2cm2 is insulated at its curved surface. The one end of rod is maintained in steam chamgber and other is maintained in ice at 0∘C (The thermal coductivity of copper is 386J/m−s.∘C). Find the temperature at a point which is at a distance of 120cm from the colder end.
A80∘CB60∘CC50∘CDnone of the aboveA metallic rod of cross-sectional area 20 cm2, with the lateral surface insulated to prevent heat loss, has one end immersed in boiling water and the other in ice water mixture. The heat conducted through the rod melts the ice at the rate of 1 gm for every 84 sec. The thermal conductivity of the rod is 160Wm−1K−1. Latent heat of ice=80 cal/gm, 1 ca=4.2 joule. What is the length (in m) of the rod?
A4B8C12D16A rod of 40 cm in length and temperature difference of 80∘C at its two ends. Another rod B of length 60cm and of temperature difference 90∘C, having the same area of cross-section. If the rate of flow of heat is the same, then the ratio of their thermal conductivities will be
A3:4B4:3C1:2D2:1
One end of a copper rod of uniform cross section and length 1.5 m is kept in contact with ice and the other end with water at 100∘C. At what point along its length should a temperature of 200∘C be maintained so that in the steady state, the mass of ice melting be equal to that of the steam produced in same interval of time. Assume that the whole system is insulated from surroundings:
[Lice=80cal/g,Lsteam=540cal/g]
View SolutionOne end of a copper rod of uniform cross-section and of length 3.1 m is kept in contact with ice and the other end with water at 100°C . At what point along it's length should a temperature of 200°C be maintained so that in steady state, the mass of ice melting be equal to that of the steam produced in the same interval of time. Assume that the whole system is insulated from the surroundings. Latent heat of fusion of ice and vaporisation of water are 80 cal/gm and 540 cal/gm respectively

View SolutionOne end of a metal rod of length 1.0 m and area of cross section 100cm2 is maintained at . 100∘C. If the other end of the rod is maintained at 0∘C , the quantity of heat transmitted through the rod per minute is (Coefficient of thermal conductivity of material of rod =100W/m−K)
View SolutionOne end of a copper rod of length 1.0 m and area of cross-section 10−3 is immersed in boiling water and the other end in ice. If the coefficient of thermal conductivity of copper is 92cal/m−s−.∘C and the latent heat of ice is 8×104cal/kg, then the amount of ice which will melt in one minute is
View Solution
As shown in Fig. AB is rod of length 30 cm and area of cross section 1.0cm2 and thermal conductivity 336 SI units. The ends A and B are maintained at temperatures 20∘C and 40∘C, respectively .A point C of this rod is connected to a box D, containing ice at 0∘C through a highly conducting wire of negligible heat capacity. The rate at which ice melts in the box is (assume latent heat of fusion for ice Lf=80cal/g)
View Solution
