A gas is to be expanded from initial state i to final state f along either path 1 or path 2 on a p-V diagram. Path 1 consists of three steps: an isothermal expansion (work is 23 J in magnitude), an adiabatic expansion (work is 35 J in magnitude), and another isothermal expansion (work is 16 J in magnitude). Path 2 consists of two steps: a pressure reduction at constant volume and an expansion at constant pressure . what is the change in the internal energy of gas along path 2 ?
To find the change in the internal energy of the gas along path 2, we need to understand the relationship between internal energy, work done, and heat transfer according to the first law of thermodynamics. The first law states:
ΔU=Q−W
Where:
- ΔU is the change in internal energy,
- Q is the heat added to the system,
- W is the work done by the system.
1. Identify the Processes in Path 2:
- Path 2 consists of two steps:
- A pressure reduction at constant volume (which means no work is done, W=0).
- An expansion at constant pressure.
2. Understand the Constant Volume Process:
- In the first step (pressure reduction at constant volume), since the volume does not change, the work done (W) is zero.
- Therefore, the change in internal energy during this step is solely dependent on the heat transfer (Q).
3. Understand the Constant Pressure Process:
- In the second step (expansion at constant pressure), the work done by the gas can be calculated using the formula:
W=PΔV
- However, we do not have specific values for pressure or volume changes in this problem.
4. Relate to Path 1:
- The change in internal energy is a state function and depends only on the initial and final states, not on the path taken.
- From the information given in path 1, we know that:
- The isothermal processes do not contribute to the change in internal energy (ΔU=0).
- The adiabatic expansion contributes a change in internal energy of −35J (since Q=0 and W=35J).
- Therefore, the total change in internal energy along path 1 is −35J.
5. Conclusion for Path 2:
- Since the change in internal energy is the same for both paths (as they connect the same initial and final states), the change in internal energy along path 2 is also:
ΔU=−35J
Final Answer:
The change in the internal energy of the gas along path 2 is −35J.
---
- ΔU is the change in internal energy,
- Q is the heat added to the system,
- W is the work done by the system.
- Path 2 consists of two steps:
- A pressure reduction at constant volume (which means no work is done, W=0).
- An expansion at constant pressure.
- In the first step (pressure reduction at constant volume), since the volume does not change, the work done (W) is zero.
- Therefore, the change in internal energy during this step is solely dependent on the heat transfer (Q).
- In the second step (expansion at constant pressure), the work done by the gas can be calculated using the formula:
W=PΔV
- However, we do not have specific values for pressure or volume changes in this problem.
- The change in internal energy is a state function and depends only on the initial and final states, not on the path taken.
- From the information given in path 1, we know that:
- The isothermal processes do not contribute to the change in internal energy (ΔU=0).
- The adiabatic expansion contributes a change in internal energy of −35J (since Q=0 and W=35J).
- Therefore, the total change in internal energy along path 1 is −35J.
- Since the change in internal energy is the same for both paths (as they connect the same initial and final states), the change in internal energy along path 2 is also:
ΔU=−35J
The change in the internal energy of the gas along path 2 is −35J.
Topper's Solved these Questions
- THE FIRST LAW OF THERMODYNAMICSBOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PRACTICE QUESTIONS ( SINGLE CORRECT CHOICE TYPE )
48 Videos
- THE FIRST LAW OF THERMODYNAMICSBOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - PRACTICE QUESTIONS ( MORE THAN ONE CORRECT CHOICE TYPE )
9 Videos
- THE FIRST LAW OF THERMODYNAMICSBOOK - RESNICK AND HALLIDAYCHAPTER - THE FIRST LAW OF THERMODYNAMICSEXERCISE - CHECK POINT
8 Videos
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)
4 Videos
- THE KINETIC THEORY OF GASESBOOK - RESNICK AND HALLIDAYCHAPTER - THE KINETIC THEORY OF GASESEXERCISE - PRACTICE QUESTIONS
72 Videos
Similar Questions
Obtain an expression for work done by a gas in an isothermal expansion.
View SolutionThe figare shows two paths that may be taken by a gas from an initial point i to final point f. Padh 1 consists of an isoubermal expansion (work is 50J in mugnitude), an isothermel compression (work is 30J in magnitude), an adiabatic expansion (work is 40J in magnitude) and dhen an adiabatic compression (work is 25J in magnitude). Find the magnitude of change in intemal energy (in J) in path 2 , i.e., in path AFGE.
'(##CEN_KSR_PHY_JEE_C15_E01_012_Q06##)'
View Solution
Knowledge Check
A system is taken from a given initial state to a given final state along various paths represented on a P-V diagram. The quantity that is independent of the path is
Aamount of heat transferred QBamount of work done WCQ but not WD(Q-W)During an adiabatic expansion of 2 moles of a gas, the change in internal energy was found –50 J . The work done during the process is
AZeroB100jC−50jD50jIn an adiabatic expansion of 2 moles of a gas, the change in its internal energy was found to be –100J. The work done in this process is :
AzeroB100 jC−1000jD200j
Work done by a gas during isothermal expansion is ______________ than that done during adiabatic expansion.
View SolutionStatement-1: The amount of work done in the isothermal expansion is greater than work done in the adiabatic system for same final volume.
Statement-2: In the adiabatic expansion of a gas temperature and pressure both decrease due to decrease in internal energy of the system.
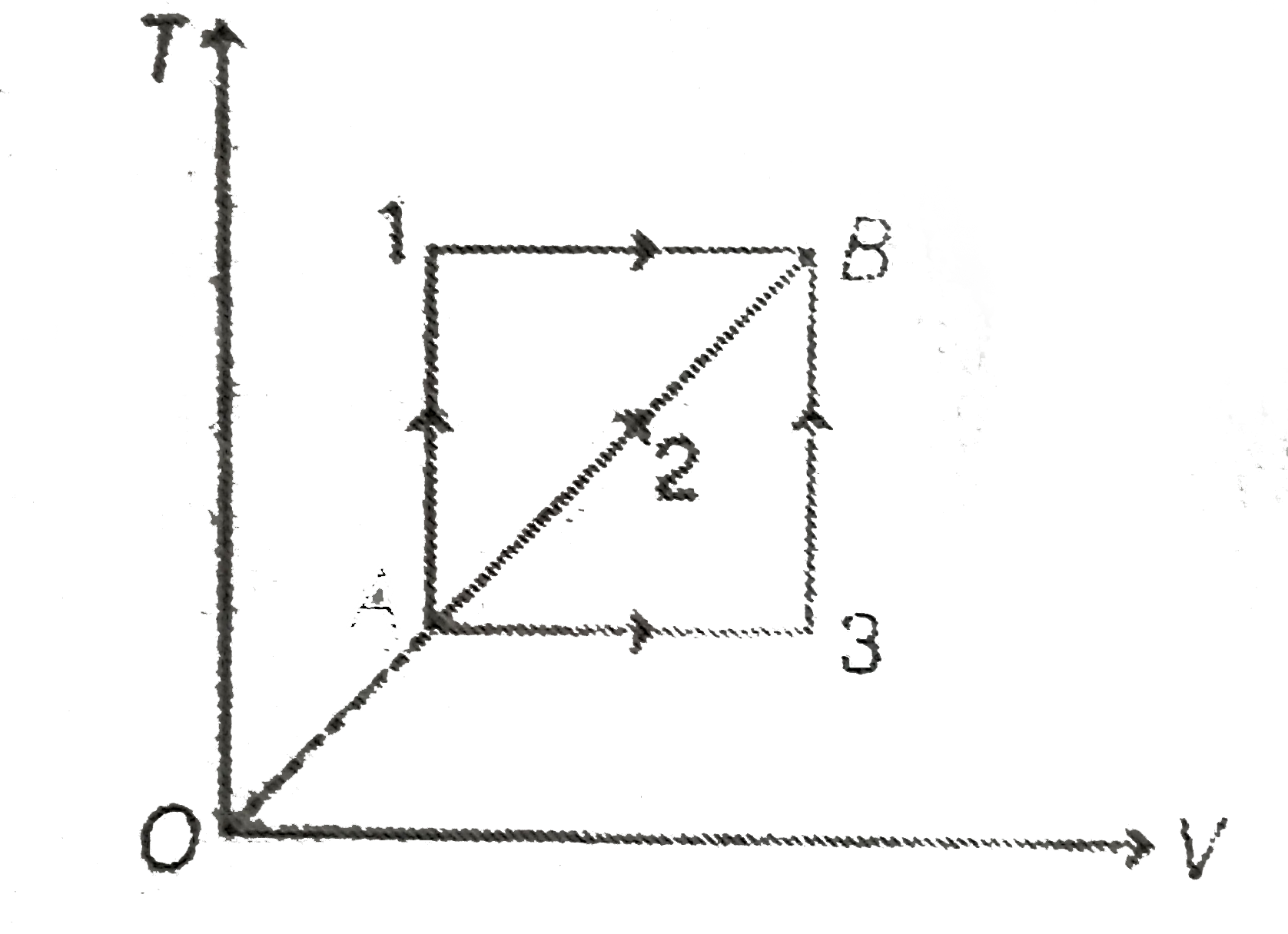
View SolutionA givne mass of a gas expands from a state A to the state B by three paths 1, 2 and 3 as shown in T-V indicator diagram. If W1,W2 and W3 respectively be the work done by the gas along the three paths, then
View SolutionAn ideal gas receives 10J of heat in a reversible isothermal expansion. Then the work done by the gas:
View SolutionA : Work done by a gas in isothermal expension is more than the work done by the gas in the same expasion adiabatically.
R : Temperature remains constant in isothermal expansion and not in adiabatic expansion.
View Solution
