Finding flux due to a point charge through a disk. The line joining the charge to the center of the disk is perpendicular to the disk.
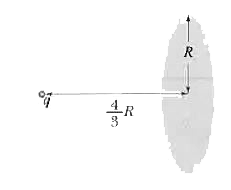
The electric field due to the point charge at the location of the ring shown is given by
E=kq(16/9)R2+x2
As we discussed before, the area of the ring is 2πdx. But the electric field is not normal to the ring. The angle can be found as shown:
cosθ=4R/3√(16R2/9)+x2
tanα=34
ϕ=∫→E.d→s
=∫0.75R0kq×(4R/3)×2πxdx[x2+(16R2/9)]×√(16R2/0)+x2=q10ε0
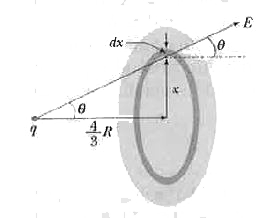
Here we divide the entire disk into thin ring and find the flux due to the charge through the thin ring.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - CHECKPOINT7videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PROBLEMS42videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)1videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
GEOMETRICAL OPTICS : REFLECTION
Similar Questions
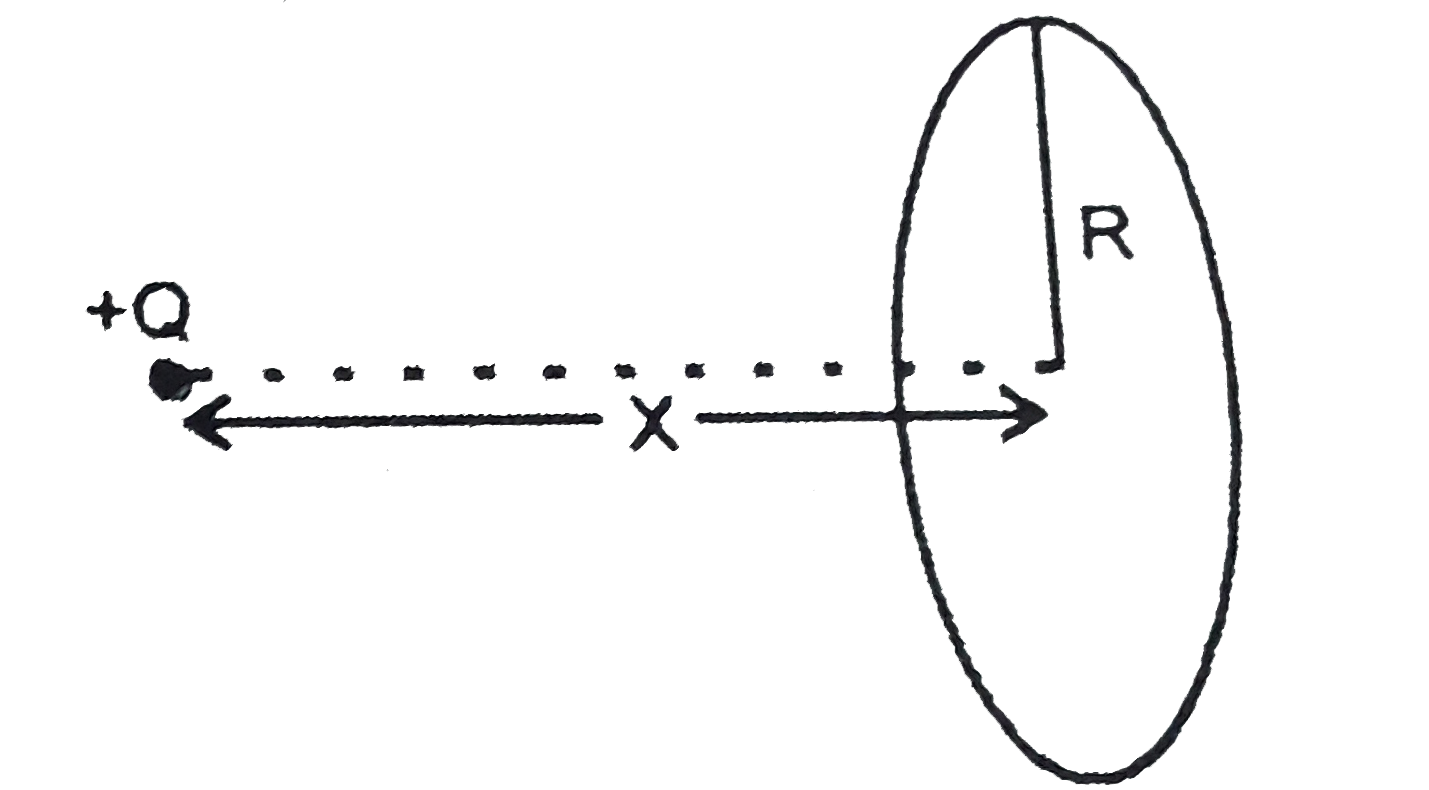
Find the electric flux due to a point charge 'Q' through the circular region of radius R if the charge is placed on the axis of ring at a distance x.
 View Solution
View SolutionFind the electric flux due to a point charge 'Q' through the circular region of radius R if the charge is placed on the axis of ring at a distance x.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Find the moment of inertia of a circular disk or solid cylinder of radius R about the axis through the centre and perpendicular to the flat surface.
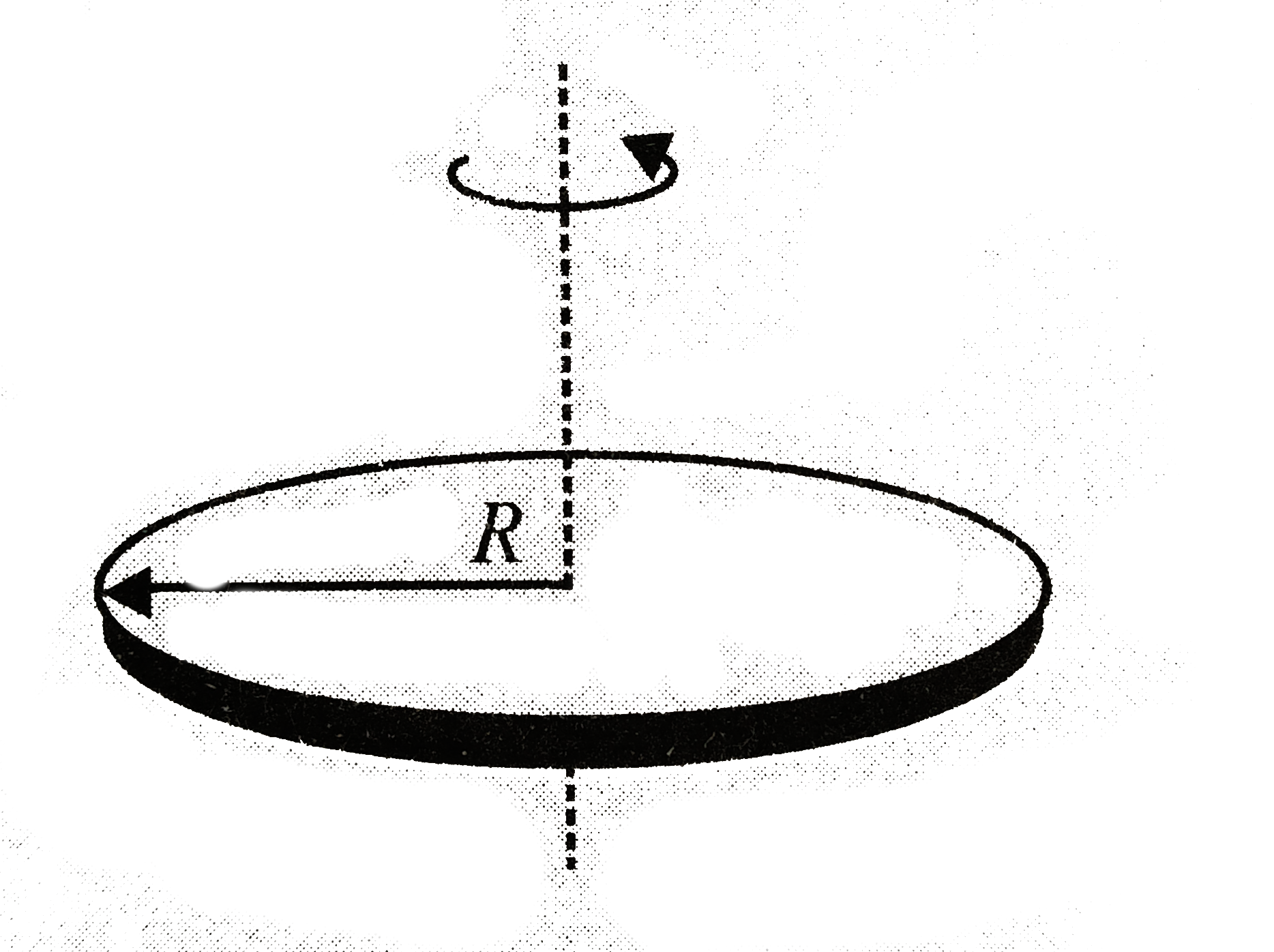 A12MR2B23MR2C32MR2DMR2
A12MR2B23MR2C32MR2DMR2 - Question 2 - Select One
Statement I:A uniformly charged disk has a pin hole at its centre. The electric field at the center of the disk is zero.
Statement II: Disk can be supposed to be made up of many rings. Also, electric field at the center of a uniformly charged ring is zero.AStatement I is true, Statement II is True, Statement II is a correct explanation for statement I.BStatement I is true, Statement II is True, Statement II is Not a correct explanation for statement I.CStatement I is True, Statement II is False.DStatement I is False, Statement II is True. - Question 3 - Select One
Two very large parallel disks of charge have their centers on the x-axis and their planes perpendicular to the x-axis. The disk that intersects x = -R has uniform positive surface charge density +σ, the disk that intersects x=+R has uniform negative surface charge density −σ. (i)
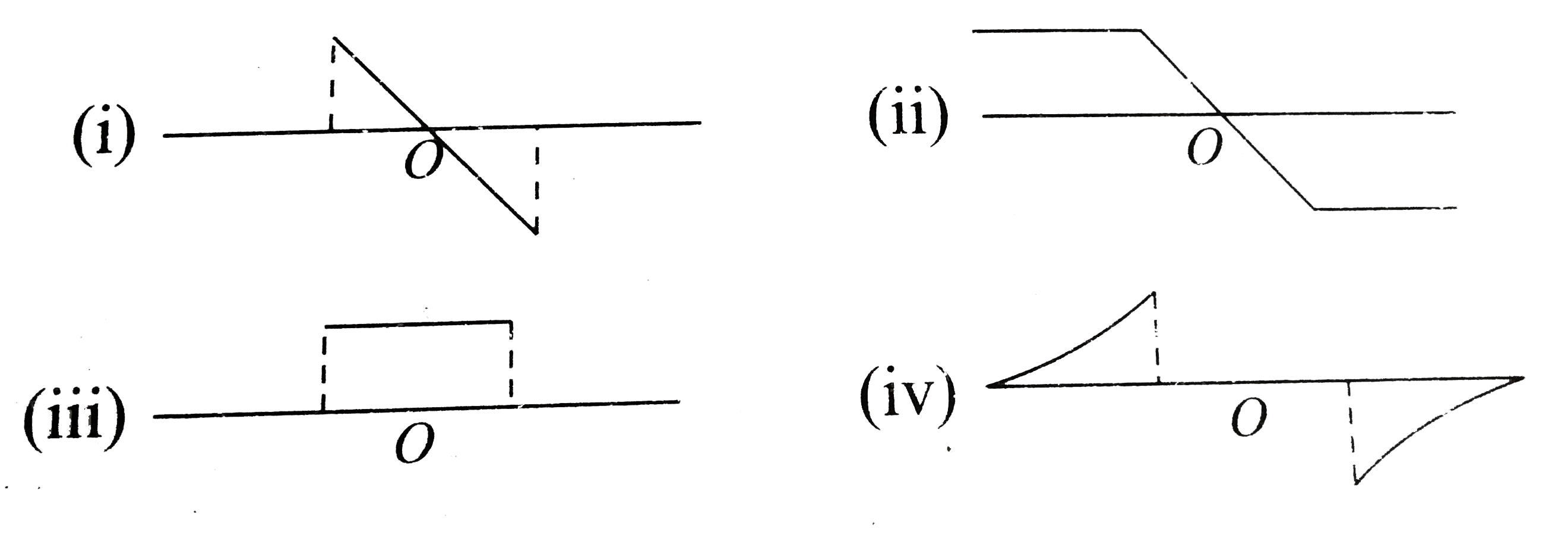 ,
,
Which graph best represents the plot of the x-component of the electric field vector on the x-axis?A(i)B(ii)C(iii)D(iv)
Find the moment of inertia of a circular disk or solid cylinder of radius R about the axis through the centre and perpendicular to the flat surface.
 View Solution
View SolutionStatement I:A uniformly charged disk has a pin hole at its centre. The electric field at the center of the disk is zero.
Statement II: Disk can be supposed to be made up of many rings. Also, electric field at the center of a uniformly charged ring is zero.View SolutionTwo very large parallel disks of charge have their centers on the x-axis and their planes perpendicular to the x-axis. The disk that intersects x = -R has uniform positive surface charge density +σ, the disk that intersects x=+R has uniform negative surface charge density −σ. (i)
 ,
,
Which graph best represents the plot of the x-component of the electric field vector on the x-axis?View SolutionNear an infinitely large flat plate with a surface charge density o on each side, the field strength is** E=δ∈nδ, while the field produced by a point charge at a distance r frorn the chargo is Prove that for a uniformly charged disk with a surface charge density a (on each side), the electric field strength on the axis of the disk is the same as for an infinitely large flat plate if the distances arc small in comparison with the disk's radius R, and is the same as for a point charge if the distances are large ** Usually the value of the field strength given in textbooks is half the one given here, since there it is assumed that the charge is on a geometric plane
View SolutionDisk 1 rotates about a smooth vertical axis with the angular velocity ω1. Disk 2 rotating with the angular velocity ω2 is kept on disk 1 while rotating in the same direction. Find the change in the rotational kinetic energy of the system given that the moments of inertia of the disks relative to the rotation axis are equal to I1andI2, respectively. The constant surface of the disks are rough.
View Solution

