Conisder an electric field →E=E0ˆx where E0 is a constant .
The flux through the shaded area (as shown in the figure) due to this field is
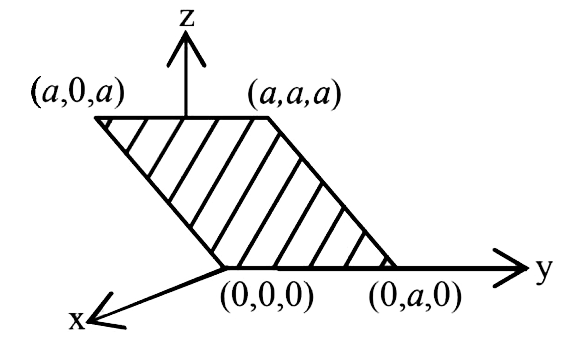
2E0a2
√2E0a2
E0a2
E0a2√2
The correct Answer is:C
Step by step video & image solution for Conisder an electric field vecE=E_0hatx where E_0 is a constant . The flux through the shaded area (as shown in the figure) due to this field is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)2videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)6videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PROBLEMS42videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)1videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
GEOMETRICAL OPTICS : REFLECTION
Similar Questions
Knowledge Check
- Question 1 - Select One
If →E=E0Xaˆi(x−mt) then flux through the shaded area is:
 AE0a2BZeroCE0a3D−E0a3
AE0a2BZeroCE0a3D−E0a3 - Question 2 - Select One
If unifrom electric filed →E=E0ˆi+2E0ˆj, where E0 is a constant, exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,0) will be.
AzeroB−E0x0C−2E0x0D−√5E0x0 - Question 3 - Select One
If uniform electric field →E=E0ˆi+2E0ˆj, where E0 is a constant exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,2x0) will be -
AzeroB−5E0x0C−3E0x0D−√5E0x0
Find the area of the shaded field shown in the given figure
 View Solution
View SolutionFind the area of the shaded field shown in the given figure.
 View Solution
View SolutionA uniform electric field →E=aˆi+bˆj intersects a surface of area A .What is the flux through this area if the surface lies in the yz plane?
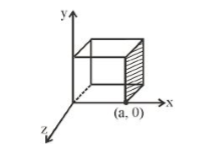
View SolutionGiven the components of an electric field as Ex=αx,Ey=0 and Ez=0, where α is a dimensional constant. Calculate the flux through each face of the cube of side a, as shown in the figure.
 View Solution
View SolutionAn electric field given →E=4.0ˆi−3.0(y2+2.0)j pierces a Gaussian cube of edge length 2.0 m and positioned as shown in the figure. (The magnitude E is in newtons per coulomb and the position z is in meters.) what is the electric flux through the (a) top face, (b) bottom face, (c) left face , (b) bottom facem (c) left face, and (d) back face ? (e) what is the net electric flux through the cube ?
 View Solution
View Solution