(a) Find the total electrostatic energy of the configuration shown in Fig. 24-58
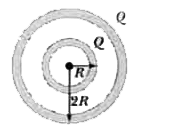
Here, we find that there are three shells of charges. In the innermost shell, charges on the inner surface of the outer shell form one shell and charges on the outer shell also form a shell. Each of these shells will have a self-energy and an interaction energy with the other two. Since there are three shells, there will be three pairs of interaction energy as seen in Fig. 24-59. So, in total, there will be six terms in the electrostatic potential energy expression.
(b) If the inner shell is earthed, find the new charges on each surface and the total electrostatic energy of the configuration.
.
.
.
Learn: Note that the interaction energies of outer shell with charge Q and with inner surface of the outer shell cancel each other. This is expected. Since there is no electric field due to the outer shell at a point inside, its interaction energy with inner shells will also be zero.
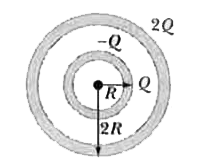
When the inner shell is earthed, its potential becomes zero. Let us assume that its charge becomes q as seen in Fig. 24-60.
Calculation:
.
Learn: Here the potential due to the inner surface and the outer surface have been combined because the outer shell is thin, and both the surfaces have the same radii. So, charge on the inner shell will be - Q/2. The facing surface will get a charge of Q/ 2, and charge on outer surface will be Q/2.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - CHECKPOINT
6 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PROBLEMS)
47 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.26 Self-energy of a uniformly charged sphere
1 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)
14 Videos
Similar Questions
Three concentric conducting spherical shells carry charges as : +4Q on the inner shell, −2Q on the middle shell and −5Q on the outer shell. The charge on the inner surface of the outer shell is
View SolutionThree concentric conducting sphereical shells carry charges +4Q on the inner shell −2Q on the middle shel and +6Q on the outer shell. The charge on the inner surface of the outer shell is
View Solution
Knowledge Check
Three concentric conducting spherical shells carry charges as : +4Q on the inner shell, −2Q on the middle shell and −5Q on the outer shell. The charge on the inner surface of the outer shell is
A0B4QC−QD−2QThree concentric conducting spherical shells carry charges +4Q on the inner shell −2Q on the middle shell and +6Q on the outer shell. The charge on the inner surface of the outer shell is
A0B4QC−QD−2Q
In (Fig. 3.73), if the inner shell has charge +q0 and the outer shell is earthed, then
 .
.
i. determine the charge on the outer shell, and
ii. find the potential of the inner shell.
View SolutionIn (Fig. 3.73), if the inner shell has charge +q0 and the outer shell is earthed, then
 .
.
i. determine the charge on the outer shell, and
ii. find the potential of the inner shell.
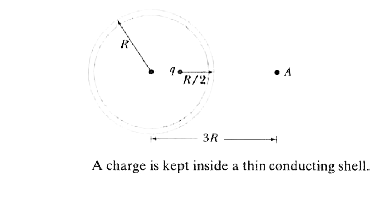
View SolutionFind the electric field at (A) (a) due to q, (b) due to charges induced on the inner surface of the shell and (c ) due to charges induced on the outer surface of the shell (Fig. 22-41).
View SolutionFind charge on each spherical shell after joining the inner most shell outer most shell by a conducting wire. Also find charges on each surface.
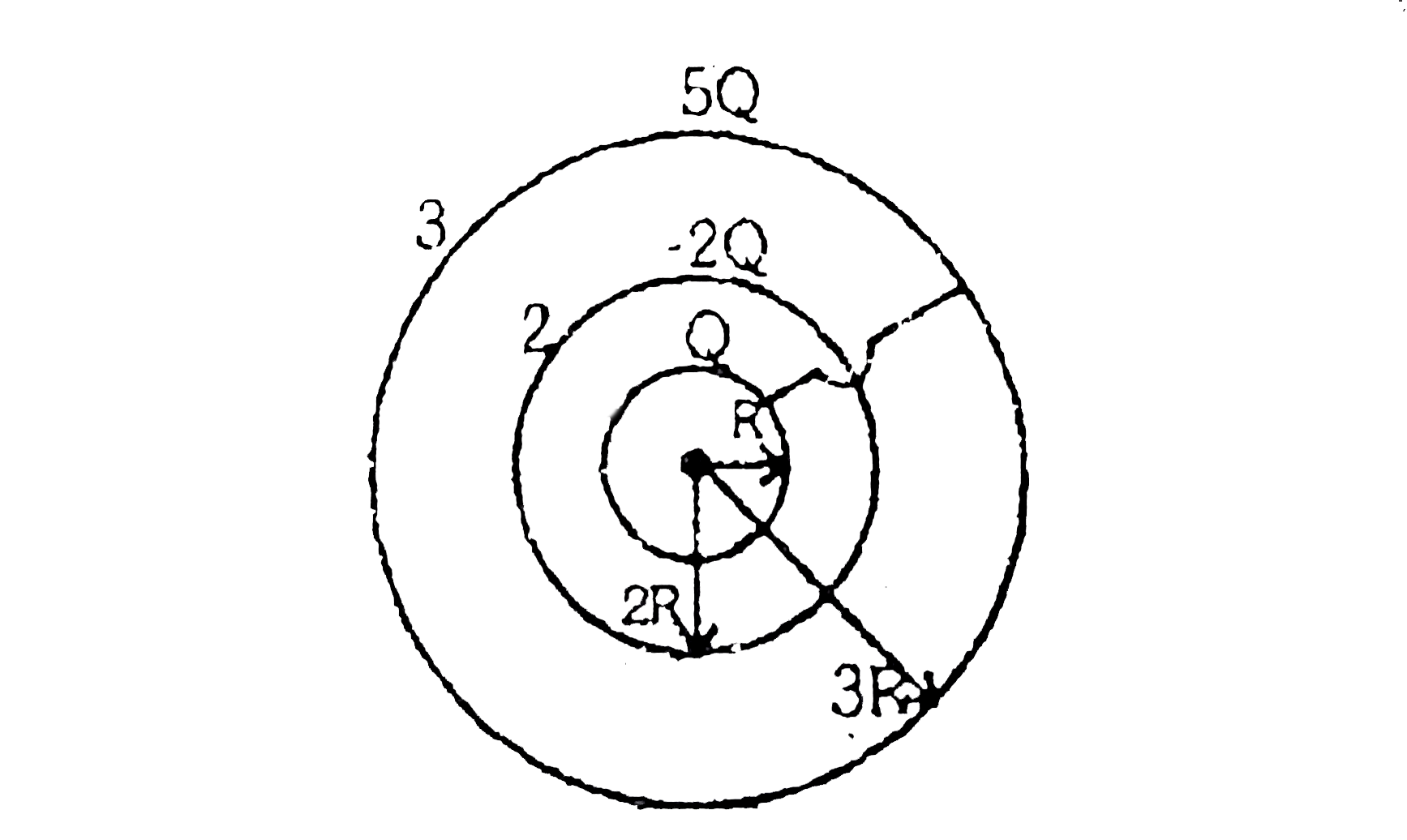
View SolutionFind charge on each spherical shell after joining the inner most shell outer most shell by a conducting wire. Also find charges on each surface.

View SolutionTwo thin conducting shells of radii R and R ar shown in figure . The outer shell carries a charge +Q and the inner shell is neutral. The inner shell is earthed with the help of switch S . Find the charge attained by the inner shell.
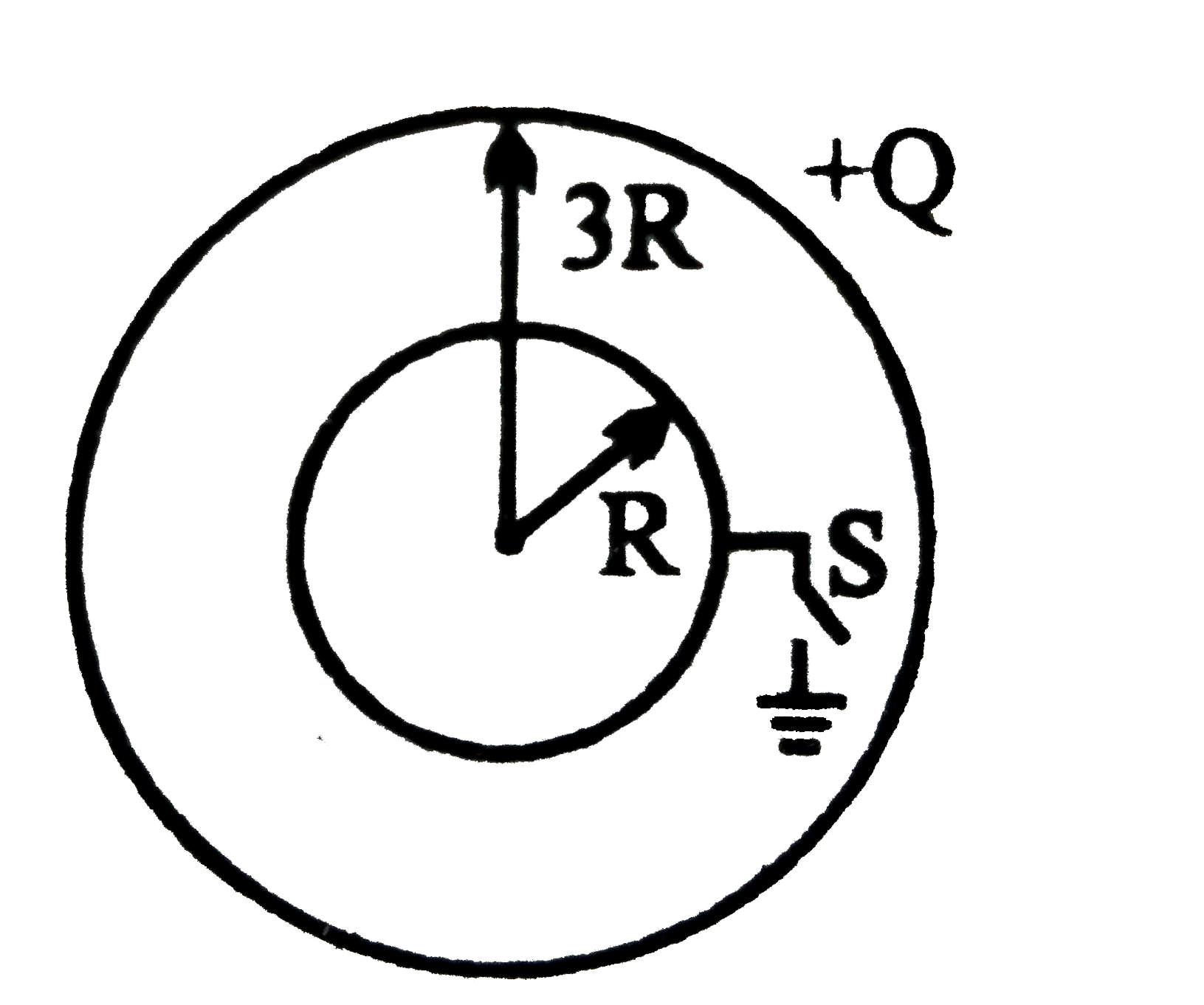 .
.
View Solution
