A positive charge +q1 is located to the left of a negative charge −q2. On a line passing through the two charges, there are two places where the total potential is zero. The first place is between the charges and is 4.00 cm to the left of the negative charge. The second place is 7.00 cm to the right of the negative charge. What is the distance between the charges?
0.637m
0.773m
0.442
0.187m
The correct Answer is:D
To solve the problem, we need to find the distance between the two charges, +q1 and −q2, given the positions where the electric potential is zero.
Step 1: Set Up the Problem
Let the distance between the two charges be x cm. The positive charge +q1 is located to the left of the negative charge −q2.
- The first point where the potential is zero (let's call it Point A) is 4.00 cm to the left of the negative charge −q2. Therefore, the distance from +q1 to Point A is x+4 cm.
- The second point where the potential is zero (let's call it Point B) is 7.00 cm to the right of the negative charge −q2. Therefore, the distance from +q1 to Point B is x+7 cm.
Step 2: Write the Equation for Point A
The total potential at Point A due to both charges is zero:
VA=Vq1+Vq2=0
The potential due to +q1 at Point A is:
Vq1=kq1x+4
The potential due to −q2 at Point A is:
Vq2=−kq24
Setting the total potential to zero:
kq1x+4−kq24=0
Cancelling k and rearranging gives:
q1x+4=q24(Equation 1)
Step 3: Write the Equation for Point B
The total potential at Point B is also zero:
VB=Vq1+Vq2=0
The potential due to +q1 at Point B is:
Vq1=kq1x+7
The potential due to −q2 at Point B is:
Vq2=−kq27
Setting the total potential to zero:
kq1x+7−kq27=0
Cancelling k and rearranging gives:
q1x+7=q27(Equation 2)
Step 4: Equate the Two Equations
From Equation 1 and Equation 2, we have:
q1q2=x+44andq1q2=x+77
Setting these equal to each other:
x+44=x+77
Step 5: Cross Multiply and Solve for x
Cross multiplying gives:
7(x+4)=4(x+7)
Expanding both sides:
7x+28=4x+28
Subtracting 4x from both sides:
3x+28=28
Subtracting 28 from both sides:
3x=0
Dividing by 3:
x=0
Step 6: Calculate the Distance Between the Charges
The distance between the charges is:
x=18.66 cm
Final Answer
The distance between the charges +q1 and −q2 is approximately 18.66 cm.
Let the distance between the two charges be x cm. The positive charge +q1 is located to the left of the negative charge −q2.
- The second point where the potential is zero (let's call it Point B) is 7.00 cm to the right of the negative charge −q2. Therefore, the distance from +q1 to Point B is x+7 cm.
The total potential at Point A due to both charges is zero:
VA=Vq1+Vq2=0
The potential due to +q1 at Point A is:
Vq1=kq1x+4
The potential due to −q2 at Point A is:
Vq2=−kq24
Setting the total potential to zero:
kq1x+4−kq24=0
Cancelling k and rearranging gives:
q1x+4=q24(Equation 1)
The total potential at Point B is also zero:
VB=Vq1+Vq2=0
The potential due to +q1 at Point B is:
Vq1=kq1x+7
The potential due to −q2 at Point B is:
Vq2=−kq27
Setting the total potential to zero:
kq1x+7−kq27=0
Cancelling k and rearranging gives:
q1x+7=q27(Equation 2)
From Equation 1 and Equation 2, we have:
q1q2=x+44andq1q2=x+77
Setting these equal to each other:
x+44=x+77
Cross multiplying gives:
7(x+4)=4(x+7)
Expanding both sides:
7x+28=4x+28
Subtracting 4x from both sides:
3x+28=28
Subtracting 28 from both sides:
3x=0
Dividing by 3:
x=0
The distance between the charges is:
x=18.66 cm
The distance between the charges +q1 and −q2 is approximately 18.66 cm.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) More than One Correct Choice Type8videos
ELECTRIC POTENTIAL
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Linked Comprehension2videos
ELECTRIC POTENTIAL
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PROBLEMS)47videos
ELECTRIC POTENTIAL
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )3videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)14videos
ELECTROMAGNETIC INDUCTION
Similar Questions
A positive charge +q1 is located to the left of a negative charge −q2. On a line passing through the two charges, there are two places where the total potential is zero. The reference is assumed to be at infinity.The first place is between the charge and is 4.00 cm to the left of the negative charge. The second place is 7.00 cm to the right of the negative charge. If q2=−12μCandq1=11×xμC, what is the value of x.
View SolutionA positive charge +q1 is located to the left of a negative charge −q2 On a line passing through the two charges, there are two places where the total potential is zero. The reference is assumed to be at infinity The first place is between the charges and is 4.00 cm to the left of the negative charge. The second place is 7.00cm to the right of the negative charge if q2=−12μC , what is the value of charge q1∈μC
View Solution
Knowledge Check
- Question 1 - Select One
The product of the magnitude of the charge and the distance between the centres of positive and negative charge is called
Acharge ratioBdipole momentCcurrent flowDmagnetic moment - Question 2 - Select One
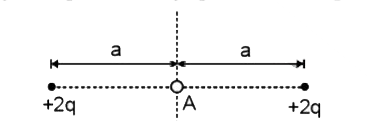
A negative point charge placed at the point A is
 Ain stable equilibrium along x-axisBin unstable equilibrium along y-axisCin stable equilibrium along y-axisDin unstable equilibrium along x-axis
Ain stable equilibrium along x-axisBin unstable equilibrium along y-axisCin stable equilibrium along y-axisDin unstable equilibrium along x-axis - Question 3 - Select One
Three charge +Q,+Q and −Q are placed at the corners of an equilateral triangle. The ratio of the force on a positive charge to the force on the negative charge will be equal to
A1B2C√3D1/√3
A negative point charge placed at the point A is
 View Solution
View SolutionA charge Q is placed at the centre of the line joining two point charges +q and +q as shown in figure. The ratio of charges Q and q is
 View Solution
View SolutionCharges Q and -2Q are placed at some distance. The locus of points in the plane of the charges where the potential is zero will be :
View SolutionTwo point charges Q1 and Q2 are positioned at points I and 2. The field intensity to the right of the charge Q2 on the line that passes through the two charges varies according to a law that is represented in the figure. The field intensity is assumed to be positive if its direction coincides with the positive direction on the x-axis. The distance between the charges is l.
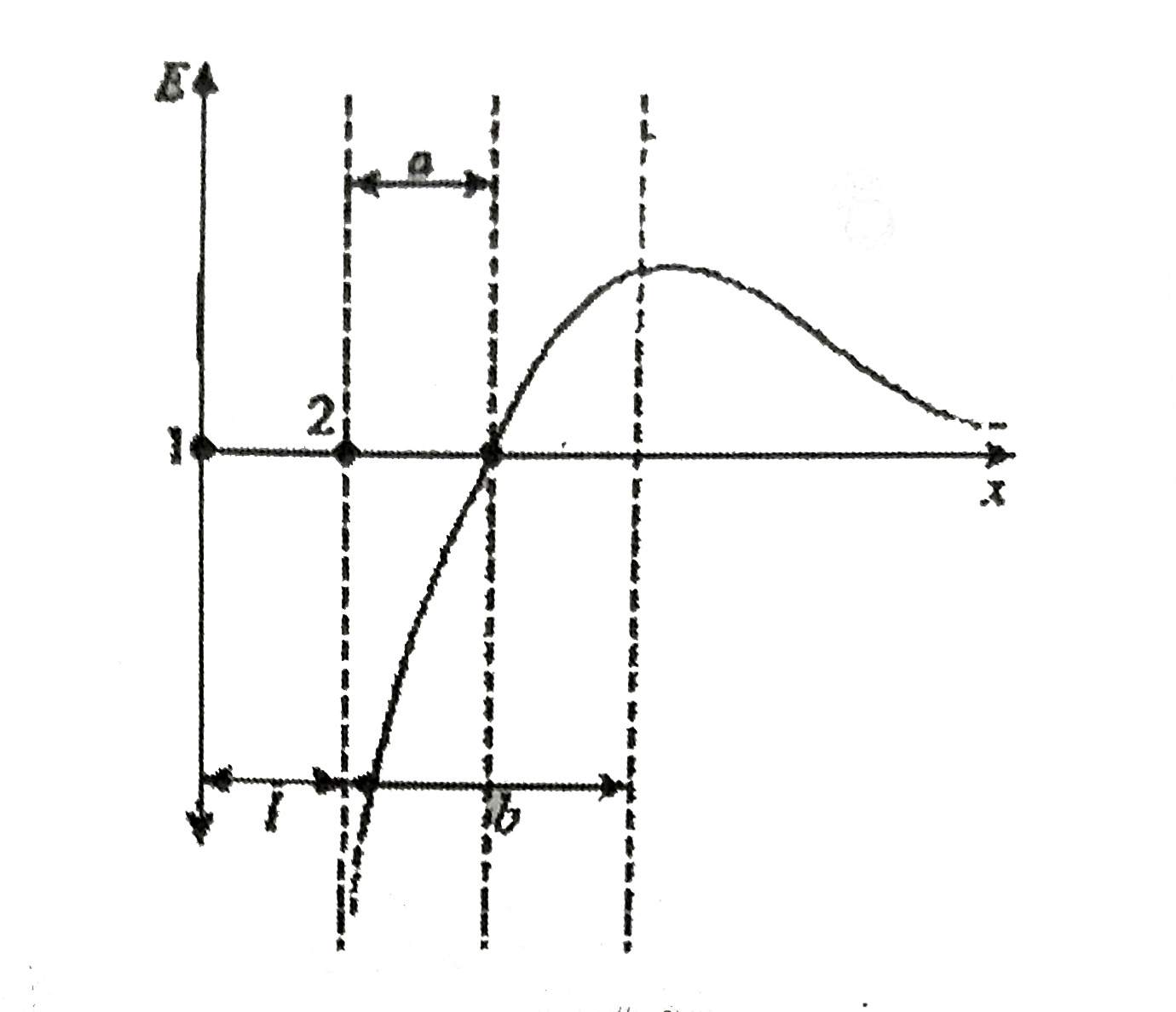
(a) Find the sign of each charge
(b) Find the ratio of the absolute values of the charges ∣∣∣Q1Q2∣∣∣
(c) Find the value of b where the field intensity is maximum
[(a) Q2 is negative and Q1 is positive (b) (l+aa)2, (c) l(l+aa)2/3−1⎤⎥ ⎥ ⎥⎦View SolutionTwo charges are placed at certain distance apart. A metallic sheet is placed between them. What will happen to the force between the charges?
View Solution

