When 233 is divided by 10, the remainder will be
2
3
4
8
The correct Answer is:A
To find the remainder when 233 is divided by 10, we can use the concept of cyclicity in powers of 2 modulo 10.
1. Identify the powers of 2 modulo 10:
- Calculate the first few powers of 2 and their remainders when divided by 10:
- 21=2 → remainder is 2
- 22=4 → remainder is 4
- 23=8 → remainder is 8
- 24=16 → remainder is 6 (since 16mod10=6)
- 25=32 → remainder is 2 (since 32mod10=2)
2. Observe the pattern:
- From the calculations, we see the remainders are:
- 2,4,8,6
- After 24, the pattern repeats every 4 terms:
- 25≡2mod10
- 26≡4mod10
- 27≡8mod10
- 28≡6mod10
- The cycle of remainders is: 2,4,8,6.
3. Determine the position of 233 in the cycle:
- Since the cycle length is 4, we need to find 33mod4:
- 33÷4=8 remainder 1 (since 33=4×8+1).
- Thus, 33mod4=1.
4. Find the corresponding remainder:
- From the cycle 2,4,8,6, the remainder corresponding to 21 (the first position in the cycle) is 2.
5. Conclusion:
- Therefore, the remainder when 233 is divided by 10 is 2.
Final Answer:
The remainder when 233 is divided by 10 is 2.
- Calculate the first few powers of 2 and their remainders when divided by 10:
- 21=2 → remainder is 2
- 22=4 → remainder is 4
- 23=8 → remainder is 8
- 24=16 → remainder is 6 (since 16mod10=6)
- 25=32 → remainder is 2 (since 32mod10=2)
- From the calculations, we see the remainders are:
- 2,4,8,6
- After 24, the pattern repeats every 4 terms:
- 25≡2mod10
- 26≡4mod10
- 27≡8mod10
- 28≡6mod10
- The cycle of remainders is: 2,4,8,6.
- Since the cycle length is 4, we need to find 33mod4:
- 33÷4=8 remainder 1 (since 33=4×8+1).
- Thus, 33mod4=1.
- From the cycle 2,4,8,6, the remainder corresponding to 21 (the first position in the cycle) is 2.
- Therefore, the remainder when 233 is divided by 10 is 2.
The remainder when 233 is divided by 10 is 2.
Similar Questions
Knowledge Check
- Question 1 - Select One
When 234 is divided by 9 , the remainder will be?
Aa) 7Bb) 8Cc) 5Dd) 6 - Question 2 - Select One
When 231 is divided by 5 the remainder is
A4B3C2D1 - Question 3 - Select One
When 231 is divided by 5 the remainder is
A4B3C2D1
When (719+2) is divided by 6 then remainder will be?
View SolutionWhen 2256 is divided by 17 the remainder would be
View SolutionWhen
 is divided by 12 then the remainder will be? View Solution
is divided by 12 then the remainder will be? View SolutionWhen
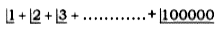 is divided by 8 then the remainder will be? View Solution
is divided by 8 then the remainder will be? View SolutionWhen 242 is divided by 33, the remainder obtained is ?
View Solution

