In ΔABC,∠B is right angle and D is the mid-point of the side AC . If AB = 6 cm , BC = 8 cm , then the length of BD is
4 cm
5 cm
8 cm
12 cm
The correct Answer is:B
To solve the problem, we need to find the length of segment BD in triangle ABC, where angle B is a right angle, D is the midpoint of side AC, AB = 6 cm, and BC = 8 cm.
1. Identify the Triangle and Given Values:
- We have triangle ABC with angle B as a right angle.
- Given: AB = 6 cm, BC = 8 cm.
2. Apply the Pythagorean Theorem:
- In a right triangle, the Pythagorean theorem states that AC2=AB2+BC2.
- Calculate AC2:
AC2=AB2+BC2=62+82=36+64=100
- Therefore, AC=√100=10 cm.
3. Determine the Length of AD and DC:
- Since D is the midpoint of AC, we have:
AD=DC=AC2=102=5 cm
4. Apply the Median Length Formula:
- In a right triangle, the median to the hypotenuse is half the length of the hypotenuse. Here, BD is the median to hypotenuse AC.
- Therefore, BD=12AC=12×10=5 cm.
5. Conclusion:
- The length of BD is 5 cm.
Final Answer:
The length of BD is 5 cm.
- We have triangle ABC with angle B as a right angle.
- Given: AB = 6 cm, BC = 8 cm.
- In a right triangle, the Pythagorean theorem states that AC2=AB2+BC2.
- Calculate AC2:
AC2=AB2+BC2=62+82=36+64=100
- Therefore, AC=√100=10 cm.
- Since D is the midpoint of AC, we have:
AD=DC=AC2=102=5 cm
- In a right triangle, the median to the hypotenuse is half the length of the hypotenuse. Here, BD is the median to hypotenuse AC.
- Therefore, BD=12AC=12×10=5 cm.
- The length of BD is 5 cm.
The length of BD is 5 cm.
Similar Questions
In the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.
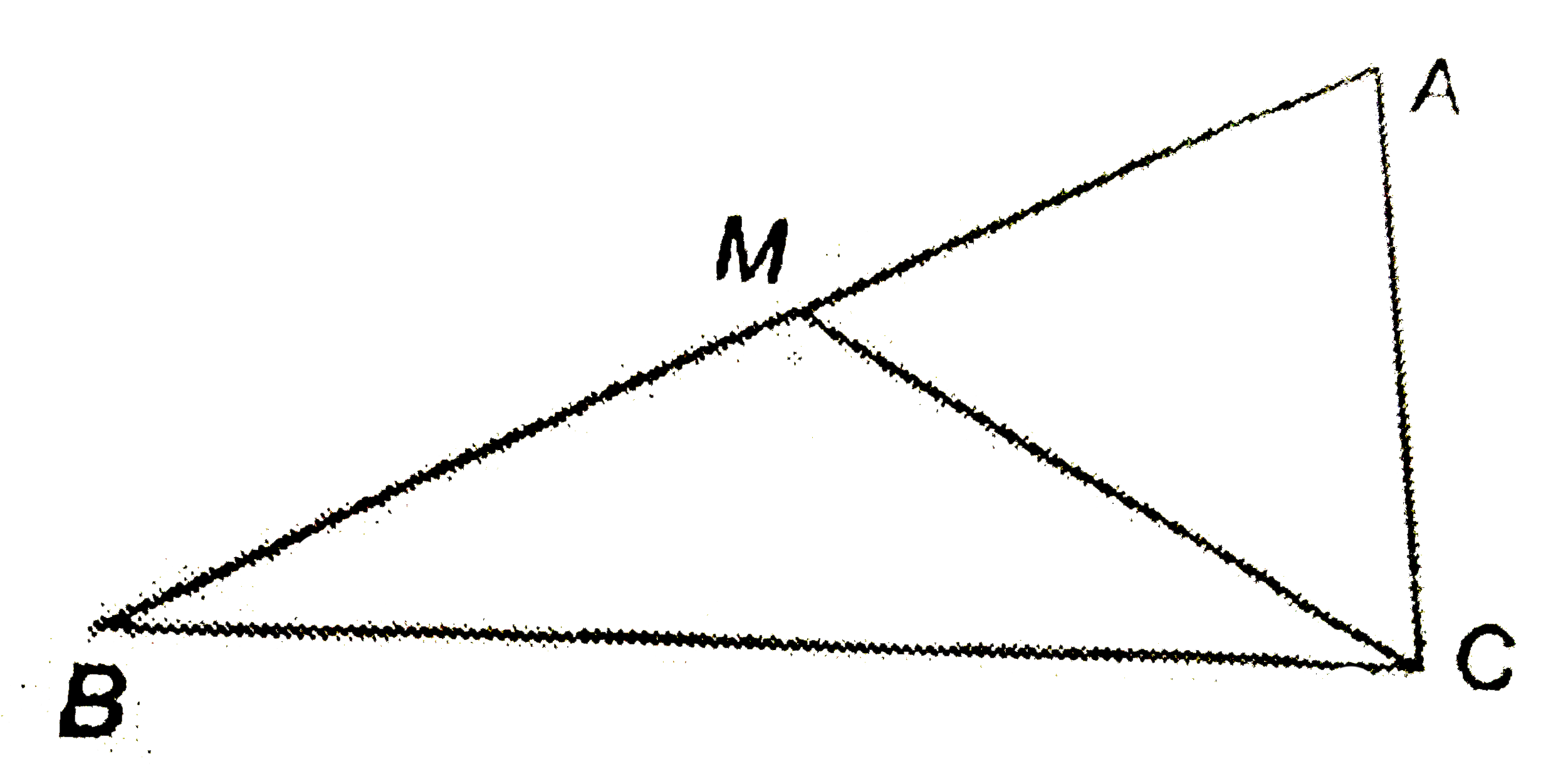 View Solution
View SolutionABC is a triangle and D is a point on the side BC. If BC = 12 cm, BD = 9 cm and ∠ADC=∠BAC, then the length of AC is equal to
View Solution
Knowledge Check
- Question 1 - Select One
In ΔABC,∠B is a right angle, AC=6 cm, D is the mid point of AC. The length of BD is
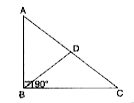 A4 cmB√6 cmC3 cmD3.5 cm
A4 cmB√6 cmC3 cmD3.5 cm - Question 2 - Select One
In ΔABC, angle B is right angle, AB = 15 cm and BC = 8 cm. The value of sin A is :
A1517B817C158D815 - Question 3 - Select One
△ABC is a right angled at A and AD is the altitude to BC. If AB= 7 cm and AC = 24 cm. Find the ratio of AD is to AM if M is the mid-point of BC.
A25:41B32:41C336625D625336
ΔABC is a right angle triangle (right angled at B), BD is perpendicular to AC. If AC = 16 cm, BC = 12 cm, find the length of CD.
View SolutionΔABC is a right angle triangle (right angled at B), BD is perpendicular to AC. If AC=16cmBC=9cm, find the length of CD.
View SolutionIn a right-angled triangle ABC, if angle B=90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
View SolutionIn ΔABC, AB=AC and D is a point on side AC such that BD = BC, If AB = 12.5 cm and BC = 5 cm, then what is the measure of DC ?
View SolutionIn a ΔABC,∠B=90∘,∠C=45∘ and D is mid point of AC. If AC = 4√2 unit then BD is
View Solution

