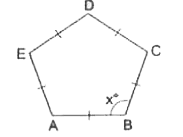
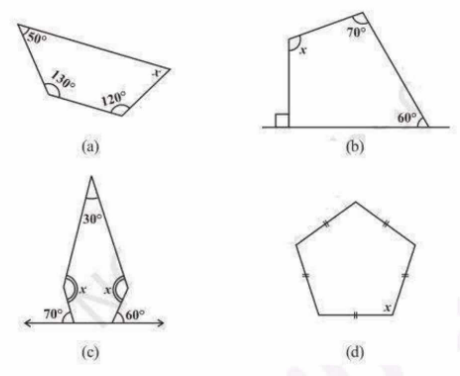
Find the angle measure x in the following figures.
Video Solution
Text Solution
(a) The given figure has 4
sides and hence it is a quadrilateral
Find the angle measure x
Using the angle sum property of a quadrilateral,
50∘+130∘+120∘+x=360∘
300∘+x=360∘
x=360∘−300∘
x=60∘
(b) Usingtheanglesum
property of a quadrilateral.
Find the angle measurexin
the following figures:
The line is perpendicular to
the base line hence, the angle formed is 90°.
90∘+60∘+70∘+x=360∘
220∘+x=360∘
220∘+x=360∘
x=360∘−220∘
x=140∘
(c) The given figure is a pentagon (number of sides =5)
Find the angle measure x in the following figures:
Angle sum of a polygon = (n−2)×180∘
=(5−2)×180∘
=3×180∘
=540∘
Sum of the interior angle of pentagon is 540^@ .
Angles at the bottom are linear pairs.
Thus, First base interior angle,
= 180^@ - 70^@ (angle of straight line is 180° )
=110∘
Also, Second base interior angle,
=180∘−60∘
=120∘
Angle sum property of a polygon = (n - 2) × 180^@
⇒30∘+x+110∘+120°+x=540∘
⇒2x+260∘=540∘
⇒2x=540∘−260∘
⇒2x=280∘
⇒x=280∘2
Therefore, x = 140∘
(d) The given figure is pentagon (number of sides =5)
Find the angle measure x in the following figures:
Sum of the interior angle of pentagon is 540^@
Angle sum of a polygon=(n−2)×180∘
=(5−2)×180∘
=3×180∘
=540∘
Let each angle of the polygon be x since it is a regular pentagon
Angle sum of a polygon =x+x+x+x+x=540∘
5x=540∘
x=540∘5
x=108∘
The givenpentagonisa
regular polygoni.e.itisboth‘equilateral’ and
‘equiangular’. Thus, the measure of each interior
angle of the pentagon is equal.
Hence each interior angle is 108∘
|
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALSBOOK - NCERTCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.3
11 Videos
- SQUARES AND SQUARE ROOTSBOOK - NCERTCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - EXERCISE 6.1
9 Videos
- VISUALISING SOLID SHAPESBOOK - NCERTCHAPTER - VISUALISING SOLID SHAPESEXERCISE - EXERCISE 10.3
8 Videos
Similar Questions
Knowledge Check
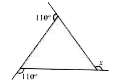
Find the measure of ∠x in the adjoining figure.
 Ax=14∘Bx=24∘Cx=34∘Dx=44∘
Ax=14∘Bx=24∘Cx=34∘Dx=44∘
Find the measure of x in each of the following
View SolutionFind the value of the unknown interior angle x in the following figures:
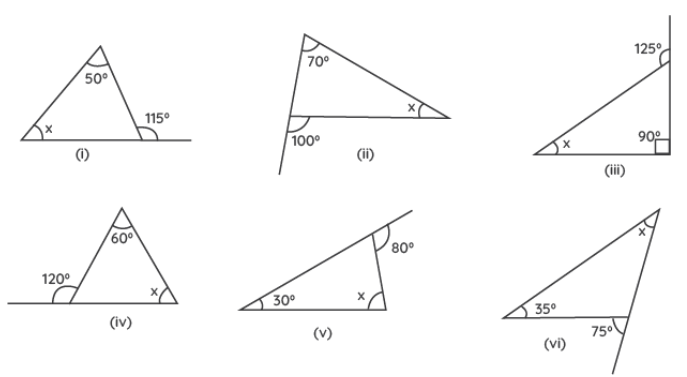
View SolutionFind the measure of angle x
View SolutionFind the areas of the following figures (All measurements are in metre)
View SolutionFind the measure of ∠LNM in the given figure.
View SolutionFind the measure of x in the given figure:
View SolutionThe adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them
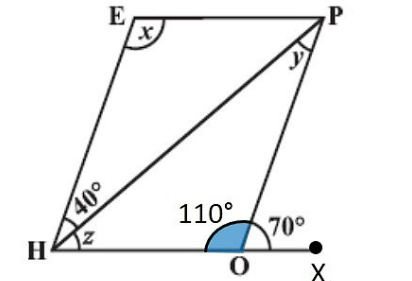 .
.
View Solution