The side BC of is produced to D. If and , what is the value (in degrees) of ?
36
48
76
84
The correct Answer is:C
To solve the problem, we need to find the value of angle BAC in triangle ABC, given that angle ACD = 114° and angle ABC = (1/2) angle BAC.
1. Identify the Angles:
- Let angle BAC = x.
- Then angle ABC = (1/2)x.
2. Use the Straight Line Property:
- Since angle ACD = 114°, we can find angle ACB using the straight line property:
Angle ACD+Angle ACB=180°
- Therefore,
114°+Angle ACB=180°
- Rearranging gives:
Angle ACB=180°−114°=66°
3. Apply the Triangle Sum Property:
- The sum of the angles in triangle ABC is 180°:
Angle ABC+Angle BAC+Angle ACB=180°
- Substituting the known values:
(12x)+x+66°=180°
4. Combine Like Terms:
- Combine the terms involving x:
12x+x=32x
- Thus, we have:
32x+66°=180°
5. Isolate x:
- Subtract 66° from both sides:
32x=180°−66°=114°
6. Solve for x:
- Multiply both sides by 23:
x=114°×23=76°
7. Conclusion:
- Therefore, the value of angle BAC is:
76°
- Let angle BAC = x.
- Then angle ABC = (1/2)x.
- Since angle ACD = 114°, we can find angle ACB using the straight line property:
Angle ACD+Angle ACB=180°
- Therefore,
114°+Angle ACB=180°
- Rearranging gives:
Angle ACB=180°−114°=66°
- The sum of the angles in triangle ABC is 180°:
Angle ABC+Angle BAC+Angle ACB=180°
- Substituting the known values:
(12x)+x+66°=180°
- Combine the terms involving x:
12x+x=32x
- Thus, we have:
32x+66°=180°
- Subtract 66° from both sides:
32x=180°−66°=114°
- Multiply both sides by 23:
x=114°×23=76°
- Therefore, the value of angle BAC is:
76°
Similar Questions
Knowledge Check
- Question 1 - Select One
The side BC of Δ ABC is produced to D. If ∠ACD=108∘ and ∠B=12∠A then ∠A is
A36∘B72∘C108∘D59∘ - Question 2 - Select One
The side BC of a ΔABC is extended to D. If ∠ACD=120∘ and ∠ABC=12∠CAB, then the value of ∠ABC is
A80∘B40∘C60∘D20∘ - Question 3 - Select One
Side BC of △ABC produced to D if ∠ACD=108∘ and ∠B=12∠A then ∠A is
A108∘B59∘C36∘D72∘
In the figure, AB = AC and BC is procured to D, if ∠CDE=20∘ and ∠BAC=80∘, then find the angle of ∠CED.
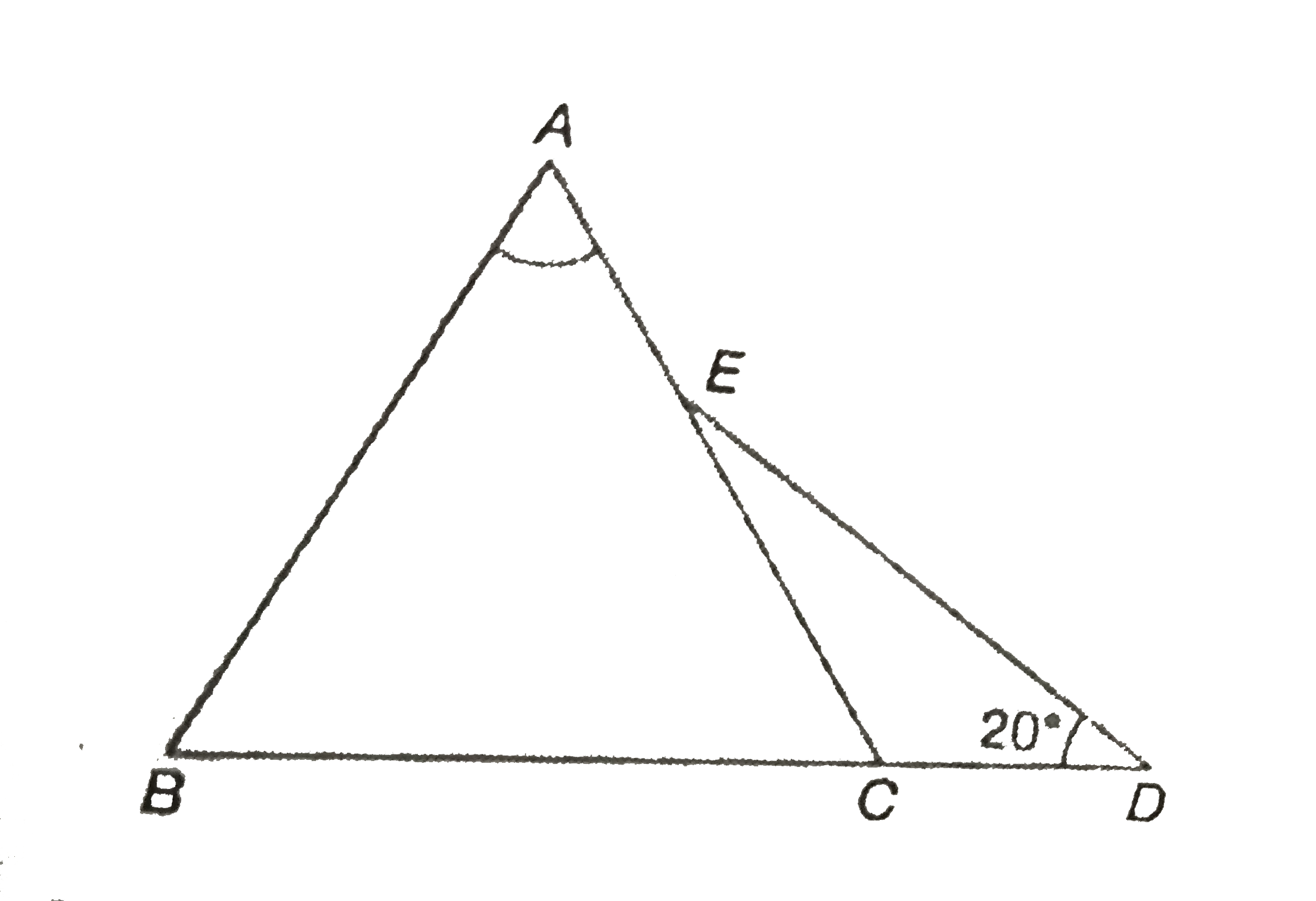 View Solution
View SolutionIn the given figure BC is produced to D and ∠BAC=40∘and∠ABC=70∘. Find the value of ∠ACD
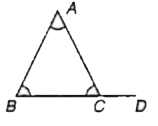 View Solution
View SolutionIn the triangle ABC, side BC is produced to D. ∠ACD=100∘ if BC = AC. Then ∠ABC is :
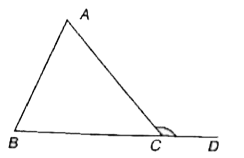 View Solution
View SolutionO is the circumcentre of a triangle ABC. If ∠BAC=85∘and∠BCA=75∘ then what is the value of ∠OAC?
View Solution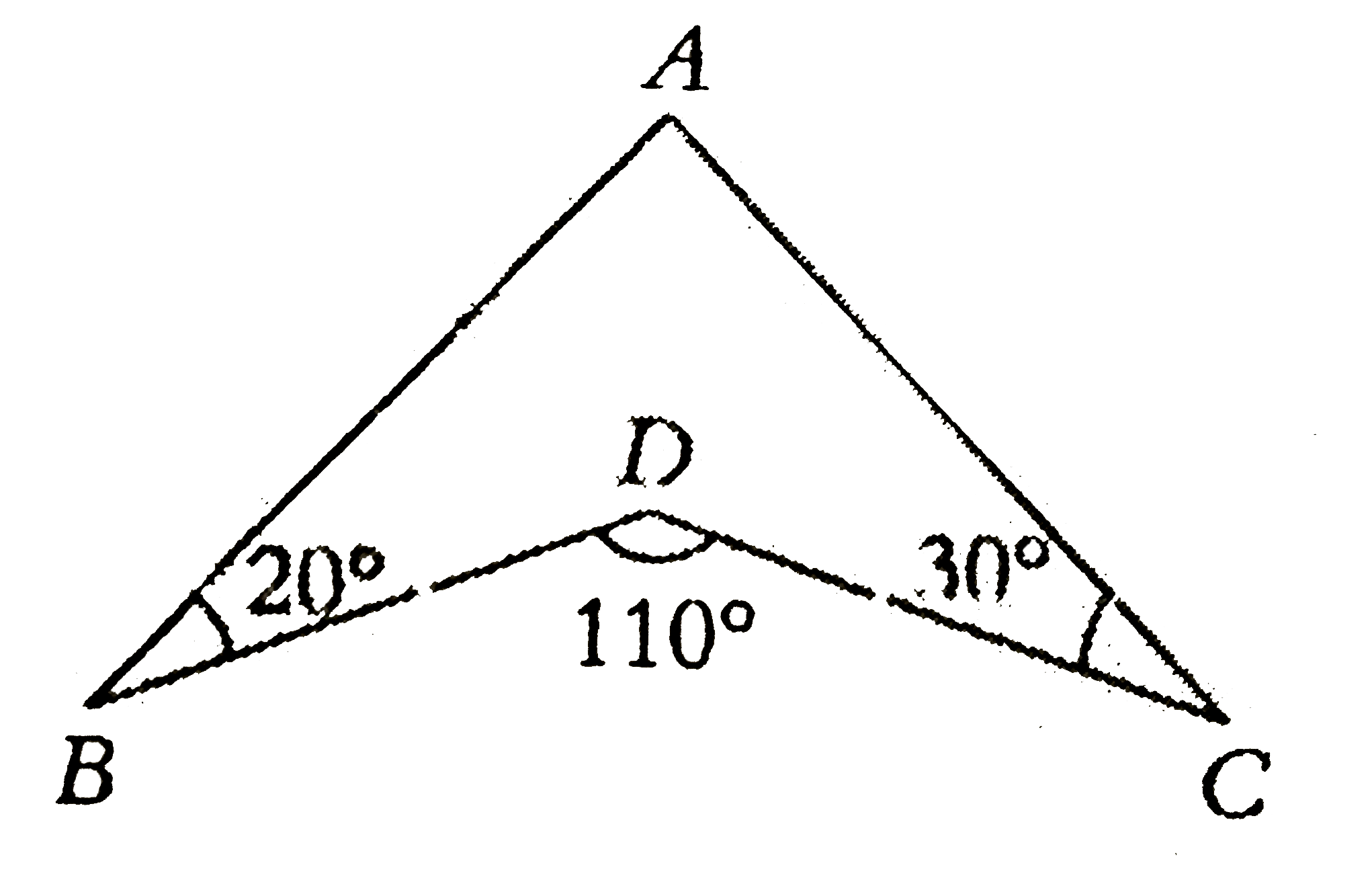
In the above figure, ∠ABD=20∘,∠BDC=110∘ and ∠DCA=30∘ . What is the value of ∠BAC ?View Solution

