Question

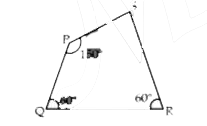
In $\Delta PQR$, PS and PT are bisectors of $\angle QPR\text{and}\angle QPS$ respectively. If $\angle QPT={30}^{\circ },PT=9cm\text{and}TR=15cm$, then what is the area (in $c{m}^2$) of $\Delta PTR$?

Options

A. 36
B. 54
C. 72
D. 216

Answer

B

Explanation

To find the area of triangle $$PTR$$, we can follow these steps:

Step 1: Understand the Triangle Configuration
We have triangle \( PQR \) with angle bisectors \( PS \) and \( PT \) where:
- \( \angle QPT = 30^\circ \)
- \( PT = 9 \, \text{cm} \)
- \( TR = 15 \, \text{cm} \)

Step 2: Identify Angles in Triangle \( PTR \)
Since \( PS \) is the angle bisector of \( \angle QPR \), we know:
- \( \angle QPT = 30^\circ \)
- Therefore, \( \angle PTS = 30^\circ \) (as \( PT \) is also a bisector)
- Since \( PS \) bisects \( \angle QPR \), \( \angle SPR = 60^\circ \) (because \( 30^\circ + 30^\circ = 60^\circ \))

Step 3: Recognize Triangle Type
In triangle \( PTR \):
- \( \angle PRT = 90^\circ \) (because \( \angle SPR + \angle QPT = 60^\circ + 30^\circ = 90^\circ \))

Step 4: Use Pythagorean Theorem
Now we can apply the Pythagorean theorem to find the length \( PR \):
\( PT^2 + TR^2 = PR^2 \)
Substituting the known values:
\( 9^2 + 15^2 = PR^2 \)
\( 81 + 225 = PR^2 \)
\( 306 = PR^2 \)
\( PR = \sqrt{306} \approx 17.5 \, \text{cm} \)

Step 5: Calculate Area of Triangle \( PTR \)
The area \( A \) of triangle \( PTR \) can be calculated using the formula:
\( A = \frac{1}{2} \times \text{base} \times \text{height} \)
Here, we can take \( PT \) as the base and \( TR \) as the height:
\( A = \frac{1}{2} \times PT \times TR \)
Substituting the values:
\( A = \frac{1}{2} \times 9 \times 15 \)
\( A = \frac{1}{2} \times 135 = 67.5 \, \text{cm}^2 \)

Step 6: Final Area Calculation
Thus, the area of triangle \( PTR \) is:
\( \text{Area} = 67.5 \, \text{cm}^2 \)