A uniform copper ring is threaded by a steadily increasing magnetic field so that the magnetic flux through the ring is changing by a constant rate. Use a voltmeter to measure the voltage across the metal ring. What do you predict?
To solve the problem, we need to analyze the situation described and apply Faraday's law of electromagnetic induction.
1. Understanding the Setup: We have a uniform copper ring that is placed in a magnetic field that is steadily increasing. This means that the magnetic flux (Φ) through the ring is changing over time.
2. Applying Faraday's Law: According to Faraday's law of electromagnetic induction, the induced electromotive force (EMF) in a closed loop is equal to the negative rate of change of magnetic flux through the loop:
EMF=−dΦBdt
where ΦB is the magnetic flux.
3. Constant Rate of Change of Flux: The problem states that the magnetic flux is changing at a constant rate. This means that dΦBdt is a constant value. Therefore, the induced EMF will also be a constant value, which is non-zero.
4. Measurement with a Voltmeter: When we connect a voltmeter across the copper ring, we are trying to measure the voltage (or EMF) induced in the ring due to the changing magnetic flux.
5. Induced Electric Field: Although there is an induced electric field in the space around the ring due to the changing magnetic flux, the voltmeter measures the potential difference across its terminals.
6. Conclusion: Since the voltmeter is connected across the ring and the induced EMF is present, the voltmeter should read a non-zero value corresponding to the induced EMF. However, if the voltmeter is not connected properly or if the induced EMF is not enclosed within the loop of the voltmeter, it may read zero.
Final Prediction:
The voltmeter will show a reading that corresponds to the induced EMF due to the changing magnetic flux through the copper ring.
EMF=−dΦBdt
where ΦB is the magnetic flux.
The voltmeter will show a reading that corresponds to the induced EMF due to the changing magnetic flux through the copper ring.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PROBLEMS
67 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
45 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)
14 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Practice Questions (Integer)
7 Videos
Similar Questions
A copper ring and a wooden ring of same dimension are placed so that there is same magnetic flux through each. Is induced current or induced EMF same in each case when flux · starts varying at the same rate in both.
View SolutionA copper ring is suspended in a vertical plane by a thread. A stell bar is passed through the ring in a horizontal direction and then a magnet is passed through it moving along the axis of ring. Will the motion of the bar and the magnet affect the position of the ring?

View Solution
Knowledge Check
Metal ring of radius R is placed perpendicular to uniform magnetic field B. Magnetic field starts changing at a rate α
AElectric field at any point on the ring is zero.BElectric field at any point on the ring is α(R)/(2)CEmf induced in the ring is zeroDEmf induced in the ring is πaR2the uniform magnetic field perpendicualr to the plane of a conducting ring of radius a change at the rate of α, then
A(a) all the points on the ring are at the same potentialB(b) the emf induced in the ring is πa2αC( c) electric field intensity E at any point on the ring is zeroD(d) E=(aα)/2The magnetic field perpendicular to the plane of a conducting ring of radius r change ate the rate dBdt
AThe emf induced in the ring is πr2dBdtBThe emf induced in the rintg is 2πrdBdtCThe potential difference between diametrically opposite points on the ring is half of the induced emf.DAll points on the ring are at the same potential.
A short bar magnet having magnetic dipole moment M is moving along the axis of a fixed conducting (non magnetic) ring of radius R. The axis of the ring is along z direction.
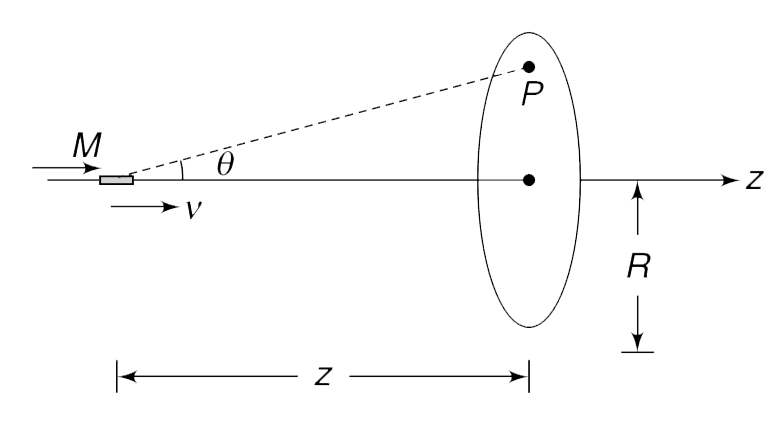
(a) Write the z component of magnetic field due to the magnetic dipole at a point P in the plane of the ring, at the instant the magnet is at a distance z from the centre of the ring. Position of point P can be defined in terms of angle θ as shown.
(b) Write the magnetic flux through the ring due to the magnetic field produced by the magnet as a function of z.
(c) Write the magnitude of emf induced in the ring at the instant shown if speed of the magnet at the moment is v.
View SolutionCan you use Ampere's law of find the magnetic field at the centre of a ring of radius R and carrying current l?
View SolutionA square loop 10 cm to a side is placed on a wooden table in a uniform magnetic field of magnitude 0.25 T. It is found that the biggest magnetic flux through the loop is measured when the loop is flat on the table. What is the flux through the loop when it is tilted such that the plane of the loop makes a 60° angle with the table?
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
View Solution
