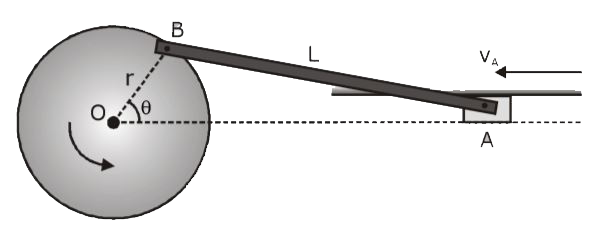
Suggest a method to locate IC for the following situations:
(a) Given the velocity of a point on the body and the angular velocity of the body.
(b) Given the lines of action of two nonparallel velocities. (c) Given the magnitude and direction of two parallel velocities.

Text Solution

Verified by Experts

(a) In this case, if ${\vec{v}}_{B}$ and $ω$ are known, the IC is located along the line drawn perpendicular to at ${\vec{v}}_{B}$ at B, such that the distance from B to the IC is ${\vec{r}}_{B / C} = v_{B} / ω$ , Fig. Note that the IC lies on that side of B which causes rotation about the IC, which is consistent with the direction of motion caused by $ω$ and ${\vec{v}}_{B}$ .
(b) Given the lines of action of two nonparallel velocities. Consider the body in Fig., where the lines of action of the velocities ${\vec{v}}_{A}$ and ${\vec{v}}_{B}$ are known. Draw two lines from points A and B that are perpendicular to ${\vec{v}}_{A}$ and ${\vec{v}}_{B}$ : Extending these perpendiculars to their point of intersection as shown locates the IC at the instant considered. The magnitudes ${\vec{r}}_{A / IC}$ and ${\vec{r}}_{B / IC}$ are generally determined from the geometry of the body and trigonometry. Furthermore, if the magnitude and sense of ${\vec{v}}_{A}$ are known, then the angular velocity of the body is determined from ${\vec{v}}_{A} = ω {\vec{r}}_{A / IC}$ Once computed, $ω$ can then be used to determine ${\vec{v}}_{B} = {\vec{r}}_{B / IC}$ .
(c) When the velocities of points A and B are par allel and have known magnitudes ${\vec{v}}_{A}$ and ${\vec{v}}_{B}$ then the location of the IC is determined by proportional triangles. Examples are shown in Fig. In both cases, ${\vec{r}}_{A / IC} = {\vec{v}}_{A} / ω$

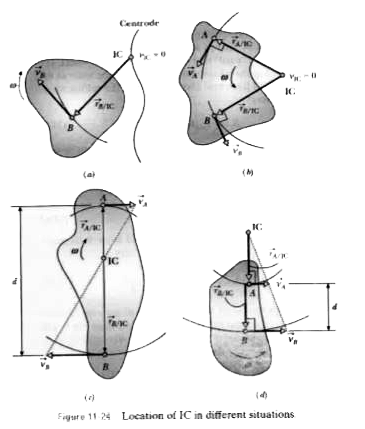
and ${\vec{r}}_{B / IC} = {\vec{v}}_{B} / ω$ . If d is a known distance between points A and B, then in Fig, ${\vec{r}}_{A / IC} + {\vec{r}}_{B / IC} = d$ and in Fig. ${\vec{r}}_{A / IC} - {\vec{r}}_{B / IC} = d$ . As a special case, note that if the body is translating, ${\vec{v}}_{A} = {\vec{v}}_{B}$ , and the IC would be located at infinity, in which case ${\vec{r}}_{A / IC} = {\vec{r}}_{B / IC} \to \infty$ . This being the case, $ω = v_{A} / \infty = v_{B} / \infty = 0$ as expected. =

Updated on:21/07/2023

Two points of a rigid body are moving as shown. The angular velocity of the body is :
.
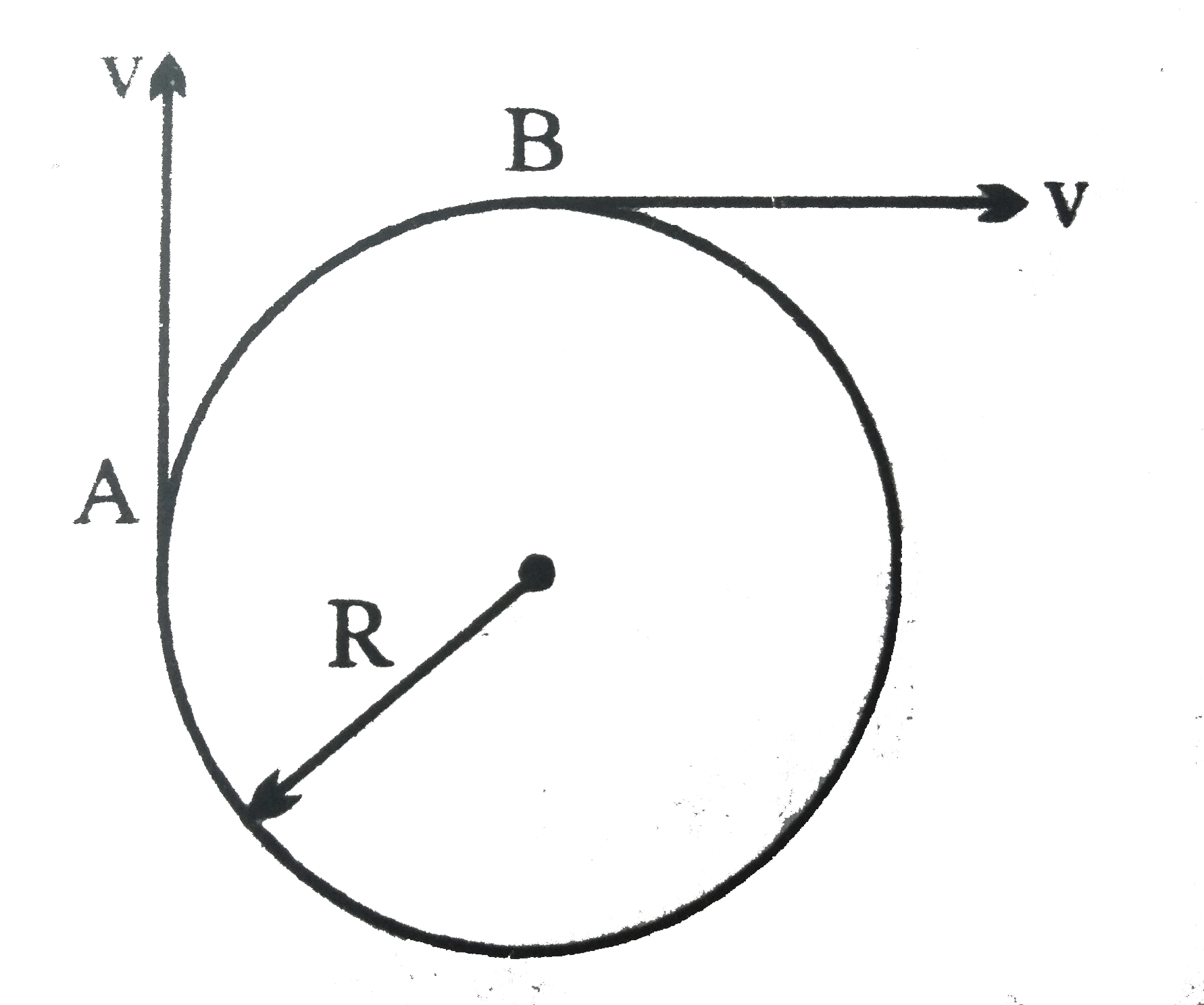A $v / 2 R$
B $v / 2$
C $2 v / R$
D $2 v / 3 R$
In a laminar flow at a given point the magnitude and direction of the velocity of the fluid
Aboth are constant
Bmagnitude is only constant
Cdirection is only constant
Dboth are not constant
The angular velocity of a rigid body about any point of that body is same :
Aonly in magnitude
Bonly in direction
Cboth in magnitude and direction necessarily
Dboth in magnitude and direction about some points but not about all points.