The packing fraction of a simple unit cell is ________.
To find the packing fraction of a simple unit cell, we can follow these steps:
1. Understanding Packing Fraction:
- The packing fraction is defined as the ratio of the volume occupied by the atoms in a unit cell to the total volume of the unit cell.
- Mathematically, it can be expressed as:
Packing Fraction=Volume of atoms in unit cellVolume of unit cell
2. Determine the Number of Atoms in a Simple Unit Cell:
- In a simple cubic unit cell, there is 1 atom per unit cell. This is because each of the 8 corner atoms contributes 18 of an atom to the unit cell:
Total atoms=8×18=1
3. Calculate the Volume of the Atom:
- The atoms can be approximated as spheres. The volume V of a single atom (sphere) is given by:
V=43πr3
- Therefore, the total volume of the atoms in the unit cell is:
Volume of atoms=1×43πr3=43πr3
4. Calculate the Volume of the Unit Cell:
- The edge length of the unit cell is denoted as A. The volume of the cubic unit cell is:
Volume of unit cell=A3
5. Relate Edge Length A to Atomic Radius r:
- In a simple cubic structure, the edge length A is related to the atomic radius r by:
A=2r
6. Substituting A in the Volume of the Unit Cell:
- Substitute A=2r into the volume of the unit cell:
A3=(2r)3=8r3
7. Calculate the Packing Fraction:
- Now, substituting the volumes into the packing fraction formula:
Packing Fraction=43πr38r3
- Simplifying this gives:
Packing Fraction=4π3×8=π6
8. Calculating the Numerical Value:
- Using π≈3.14:
Packing Fraction≈3.146≈0.524
- To express this as a percentage:
Packing Fraction (percentage)≈0.524×100≈52.4%
Final Answer:
The packing fraction of a simple unit cell is approximately 0.524 or 52.4%.
- The packing fraction is defined as the ratio of the volume occupied by the atoms in a unit cell to the total volume of the unit cell.
- Mathematically, it can be expressed as:
Packing Fraction=Volume of atoms in unit cellVolume of unit cell
- In a simple cubic unit cell, there is 1 atom per unit cell. This is because each of the 8 corner atoms contributes 18 of an atom to the unit cell:
Total atoms=8×18=1
- The atoms can be approximated as spheres. The volume V of a single atom (sphere) is given by:
V=43πr3
- Therefore, the total volume of the atoms in the unit cell is:
Volume of atoms=1×43πr3=43πr3
- The edge length of the unit cell is denoted as A. The volume of the cubic unit cell is:
Volume of unit cell=A3
- In a simple cubic structure, the edge length A is related to the atomic radius r by:
A=2r
- Substitute A=2r into the volume of the unit cell:
A3=(2r)3=8r3
- Now, substituting the volumes into the packing fraction formula:
Packing Fraction=43πr38r3
- Simplifying this gives:
Packing Fraction=4π3×8=π6
- Using π≈3.14:
Packing Fraction≈3.146≈0.524
- To express this as a percentage:
Packing Fraction (percentage)≈0.524×100≈52.4%
The packing fraction of a simple unit cell is approximately 0.524 or 52.4%.
Topper's Solved these Questions
- SOLID STATEBOOK - MODERN PUBLICATIONCHAPTER - SOLID STATEEXERCISE - QUICK MEMORY TEST (C. CHOOSE THE CORRECT ALTERNATIVE)
12 Videos
- SOLID STATEBOOK - MODERN PUBLICATIONCHAPTER - SOLID STATEEXERCISE - REVISION EXERCISES (OBJECTIVE QUESTIONS) (MULTIPLE CHOICE QUESTIONS)
39 Videos
- SOLID STATEBOOK - MODERN PUBLICATIONCHAPTER - SOLID STATEEXERCISE - QUICK MEMORY TEST (A. SAY TRUE OR FALSE)
12 Videos
- POLYMERSBOOK - MODERN PUBLICATIONCHAPTER - POLYMERSEXERCISE - Competition file (OBJECTIVE TYPE QUESTIONS) (C. MULTIPLE CHOICE QUESTIONS)(Integer Type Questions)
6 Videos
- SOLUTIONSBOOK - MODERN PUBLICATIONCHAPTER - SOLUTIONSEXERCISE - UNIT PRACTICE TEST
14 Videos
Similar Questions
Knowledge Check
Stracture of unit cell is described in the given figure packing fraction of the unit cell is?
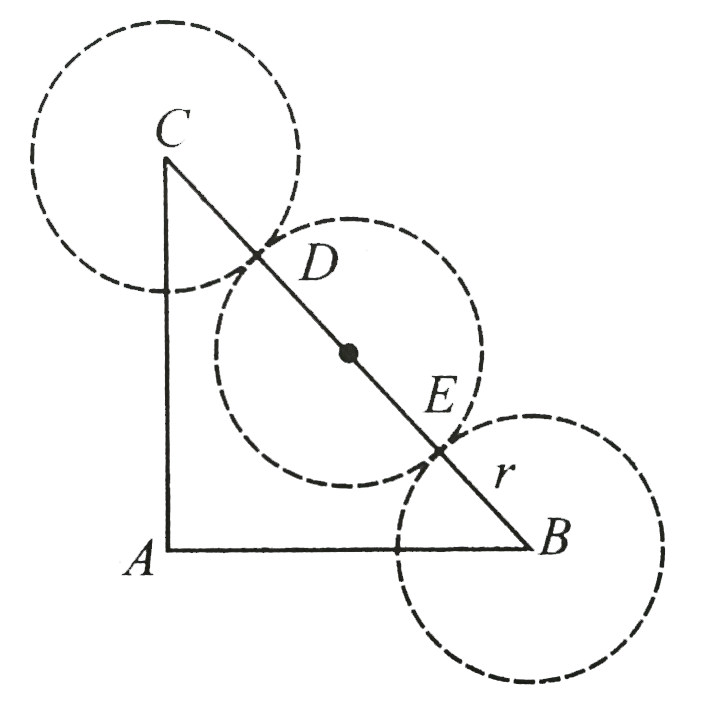 A0.521B0.907C0.093D0.745
A0.521B0.907C0.093D0.745The packing fraction of the primitive cubic unit cell is
A0.283B0.321C0.523D0.685The packing fraction for a body-centred cube is
A0.42B0.53C0.68D0.82
Calculate the packing fraction for the Ca unit cell, given that Ca crystallizes in a face-centered cubic unit cell.
View SolutionThe packing fractionin fcc and hcp structure is same. Moreover, this is the highest packing fraction of all the possible unit cells with same atoms. Can you explain this ?
View SolutionAssertion (A): The packing efficiency of simple cubic lattice is 52.4%.
Reason (R): The number of atoms per unit cell is 2.
View SolutionThe packing fraction of the element that crystallizes in simple cubic arrangement is
View Solution(A) Packing fraction of Fcc and hcp unit cell are same.
(R) Both fcc and hcp unit cell have same packing pattern i.e. ABCABCABC…….
View Solution
