In a body centred unit cell, the number of atoms present is
1
2
3
4
The correct Answer is:B
To determine the number of atoms present in a body-centered cubic (BCC) unit cell, we can follow these steps:
1. Identify the Structure of BCC:
In a body-centered cubic unit cell, there is one atom located at the center of the cube and one atom at each of the eight corners of the cube.
2. Count the Atoms at the Corners:
Each corner of the cube has an atom, and since there are 8 corners, we initially have 8 atoms from the corners.
3. Determine the Contribution of Corner Atoms:
Each corner atom is shared among 8 adjacent unit cells. Therefore, the contribution of each corner atom to the unit cell is 18.
- Total contribution from corner atoms = Number of corner atoms × Contribution per corner atom
- Total contribution from corner atoms = 8×18=1 atom.
4. Count the Atom at the Center:
The atom located at the center of the cube is not shared with any other unit cell. Therefore, its contribution is 1.
5. Calculate the Total Number of Atoms:
Now, we can sum the contributions from the corner atoms and the center atom:
- Total number of atoms in BCC = Contribution from corner atoms + Contribution from center atom
- Total number of atoms in BCC = 1+1=2.
Final Answer:
The number of atoms present in a body-centered cubic unit cell is 2.
---
In a body-centered cubic unit cell, there is one atom located at the center of the cube and one atom at each of the eight corners of the cube.
Each corner of the cube has an atom, and since there are 8 corners, we initially have 8 atoms from the corners.
Each corner atom is shared among 8 adjacent unit cells. Therefore, the contribution of each corner atom to the unit cell is 18.
- Total contribution from corner atoms = Number of corner atoms × Contribution per corner atom
- Total contribution from corner atoms = 8×18=1 atom.
The atom located at the center of the cube is not shared with any other unit cell. Therefore, its contribution is 1.
Now, we can sum the contributions from the corner atoms and the center atom:
- Total number of atoms in BCC = Contribution from corner atoms + Contribution from center atom
- Total number of atoms in BCC = 1+1=2.
The number of atoms present in a body-centered cubic unit cell is 2.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - SOLID STATEEXERCISE - REVISION EXERCISES (OBJECTIVE QUESTIONS) (MATCHING TYPE QUESTIONS)6videos
SOLID STATE
- BOOK - MODERN PUBLICATIONCHAPTER - SOLID STATEEXERCISE - REVISION EXERCISES (OBJECTIVE QUESTIONS) (PASSAGE BASED QUESTIONS)10videos
SOLID STATE
- BOOK - MODERN PUBLICATIONCHAPTER - SOLID STATEEXERCISE - QUICK MEMORY TEST (C. CHOOSE THE CORRECT ALTERNATIVE)12videos
SOLID STATE
- BOOK - MODERN PUBLICATIONCHAPTER - POLYMERSEXERCISE - Competition file (OBJECTIVE TYPE QUESTIONS) (C. MULTIPLE CHOICE QUESTIONS)(Integer Type Questions)6videos
POLYMERS
- BOOK - MODERN PUBLICATIONCHAPTER - SOLUTIONSEXERCISE - UNIT PRACTICE TEST14videos
SOLUTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In a face centred unit cell (fcc), the number of atoms present is :
A4B2C3D5 - Question 2 - Select One
In a face centered unit cell (fcc) the number of atoms present
A4B2C3D5 - Question 3 - Select One
In a body centred cubic arrangement, the number of atoms per unit cell is-
A8B2C1D4
Tungsten crystallises in a body centred cubic unit cell. If the edge of the unit cell is 316.5 pm, what is the radius of tungsten atom ?
View SolutionIn a unit cell, atoms A, B, C and D are present at comers, face centres, body - centre and edge - centre respectively in a cubic unit cell. The total number of atoms present per unit cell is
View SolutionPerovaskite, a mineral containing calcium, oxygen & titanium crystallizes in the given unit cell
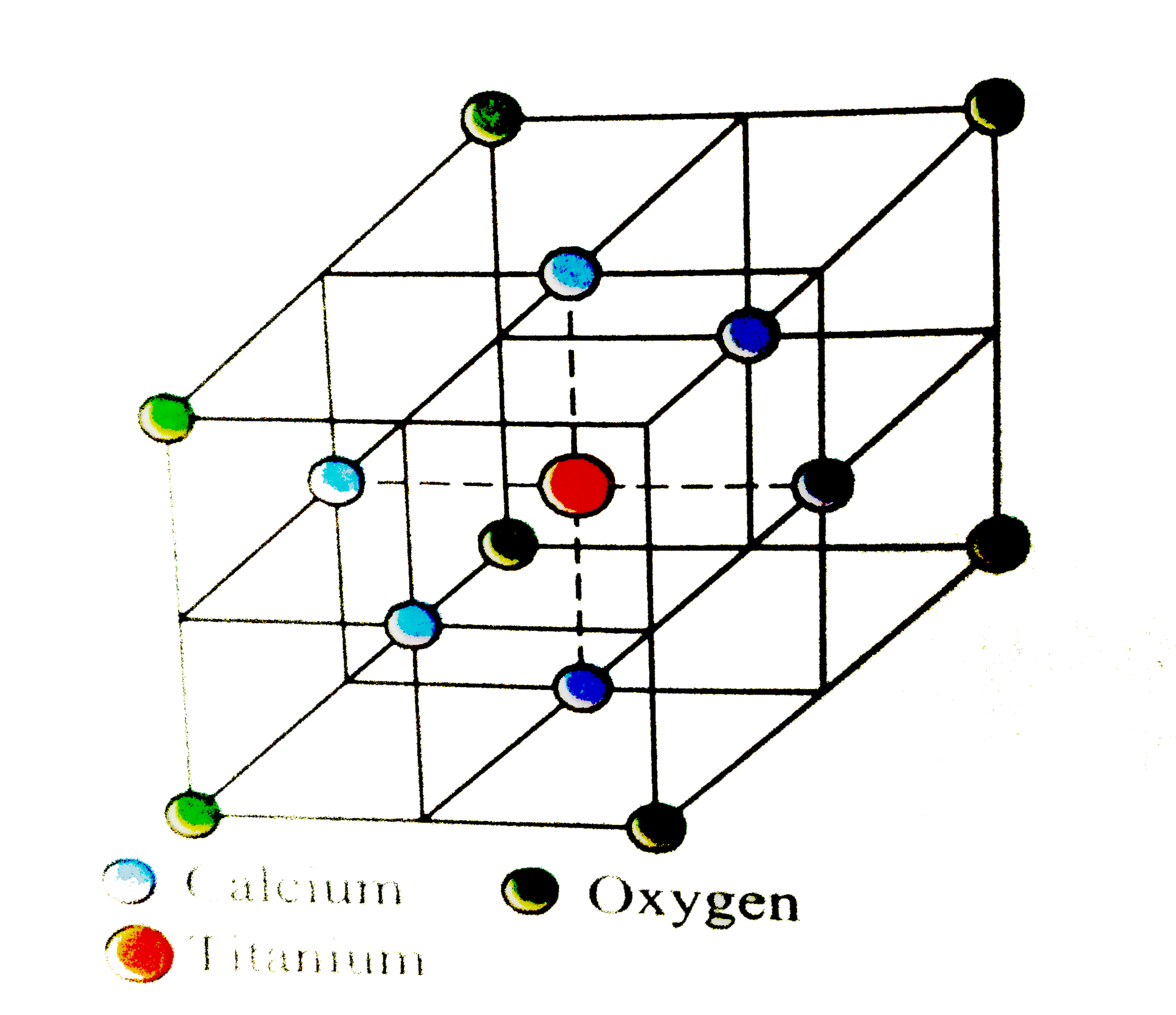
Total number of atom present in a unit cell isView SolutionIn a body centred cubic cell an atom at the body of centre is shared by-
View SolutionIn a simple cubic, body-centred cubic and face-centred cubic structure, the ratio of the number of atoms present is respectively
View Solution

