The ages of the students of a class form an A.P. whose common difference is 4 months. If the youngest student is 8 years old and the sum of the ages of all the students of the class is 168 years, find the number of students in the class.
The correct Answer is:16
To solve the problem, we need to find the number of students in a class whose ages form an arithmetic progression (A.P.). Here are the steps to find the solution:
Step 1: Identify the parameters of the A.P.
- The youngest student is 8 years old, which we can denote as a=8 years.
- The common difference d=4 months. We need to convert this into years for consistency:
d=412=13 years
Step 2: Use the formula for the sum of the first n terms of an A.P.
The formula for the sum Sn of the first n terms of an A.P. is given by:
Sn=n2(2a+(n−1)d)
We know that the sum of the ages of all the students is 168 years, so we can set up the equation:
168=n2(2(8)+(n−1)(13))
Step 3: Simplify the equation
Substituting a=8 and d=13:
168=n2(16+n−13)
Multiply both sides by 2 to eliminate the fraction:
336=n(16+n−13)
Now, multiply through by 3 to eliminate the fraction:
1008=3n(16+n−13)
This simplifies to:
1008=48n+n(n−1)
Rearranging gives:
n2−n+48n−1008=0
n2+47n−1008=0
Step 4: Solve the quadratic equation
We can use the quadratic formula n=−b±√b2−4ac2a:
Here, a=1,b=47,c=−1008:
b2−4ac=472−4×1×(−1008)=2209+4032=6241
Now, calculate n:
n=−47±√62412×1=−47±792
Calculating the two possible values:
1. n=322=16
2. n=−1262=−63 (not valid since number of students cannot be negative)
Step 5: Conclusion
Thus, the number of students in the class is:
16
- The youngest student is 8 years old, which we can denote as a=8 years.
- The common difference d=4 months. We need to convert this into years for consistency:
d=412=13 years
The formula for the sum Sn of the first n terms of an A.P. is given by:
Sn=n2(2a+(n−1)d)
We know that the sum of the ages of all the students is 168 years, so we can set up the equation:
168=n2(2(8)+(n−1)(13))
Substituting a=8 and d=13:
168=n2(16+n−13)
Multiply both sides by 2 to eliminate the fraction:
336=n(16+n−13)
Now, multiply through by 3 to eliminate the fraction:
1008=3n(16+n−13)
This simplifies to:
1008=48n+n(n−1)
Rearranging gives:
n2−n+48n−1008=0
n2+47n−1008=0
We can use the quadratic formula n=−b±√b2−4ac2a:
Here, a=1,b=47,c=−1008:
b2−4ac=472−4×1×(−1008)=2209+4032=6241
Now, calculate n:
n=−47±√62412×1=−47±792
Calculating the two possible values:
1. n=322=16
2. n=−1262=−63 (not valid since number of students cannot be negative)
Thus, the number of students in the class is:
16
Topper's Solved these Questions
- SEQUENCES AND SERIESBOOK - MODERN PUBLICATIONCHAPTER - SEQUENCES AND SERIESEXERCISE - CHECK YOUR UNDERSTANDING
10 Videos
- SEQUENCES AND SERIESBOOK - MODERN PUBLICATIONCHAPTER - SEQUENCES AND SERIESEXERCISE - COMPETITION FILE
21 Videos
- SEQUENCES AND SERIESBOOK - MODERN PUBLICATIONCHAPTER - SEQUENCES AND SERIESEXERCISE - EXERCISE
7 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Chapter Test
11 Videos
- SETS BOOK - MODERN PUBLICATIONCHAPTER - SETS EXERCISE - CHAPTER TEST 1
12 Videos
Similar Questions
A class consists of a number of boys whose ages are in A.P., the common difference being four months. If the youngest boy is just eight years old and if the sum of the ages is 168 years, then number of boys in the class, are 16 (b) 18 (c) 20 (d) None of these
View SolutionThe average age of all the students of a class is 22 years. The average age of boys of the class is 24 years and that of the girls is 20 years. If the number of girls in the clss is 30, then the find the number of studnets in the class.
View Solution
Knowledge Check
6 months a go the present age of the student of class 10th was 14 years 6 months hence the age of the same students will be :
A15 yearsB15(1/2) yearsC20 yearsDnone of theseThe average age of all the 20 students of a class is 24. The minimum age of a student is 18 and the maximum age of another student in the same class is 30 years. When the two students whose average age was 26 years resticted from the class but later on one of the resticated student was readmitted. Now the average age of the class is:
A23.89 yearsB28.39 yearsC25 yearsDcan't be determinedThe average age of all the 20 students of a class is 24. The minimum age of a student is 18 and the maximum age of another student in the same class is 30 years. When the two students whose average age was 26 years resticted from the class but later on one of the resticated student was readmitted. Now the average age of the class is:
A23.89 yearsB28.39 yearsC25 yearsDCan't determined
The average age of all the students of a class is 18 years. The average age of boys of the class is 20 years and that of the girls is 15 years. If the number of girls in the class is 20, then find the number of boys in the class. (a) 15 (b) 30 (c) 45 (d) 50
View SolutionThe given bar graph, shows the number of students in different classes.
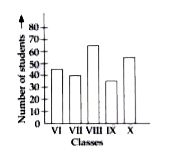
Find the total number of students in the classes VIII to X.
View SolutionIf the average weight of the students of a class is 15kg, the average weight of the students of another class is 30kg and average weight of the students of both the classes is 25kg, then find the ratio of the number of students of the first class to the another class.
View SolutionThe mean age of a class is 16 years. If the class teacher aged 40 years old is also included, the mean age increases to 17 years. The number of students in the class are :
View SolutionThe students of a class donated a sum of Rs 2, 209. If each student donated as many rupees as the number of students in the class, then the number of students in the class is
View Solution
