A horizontal conveyor belt is moving at a speed of 5m/s. A box of mass 20kg is gently placed on this belt. Box first slips on the belt and finally comes to rest with respect to belt. If box takes time 0.1 s to stop slipping on the belt, then what will be the distance travelled by the box during this interval?
To solve the problem step-by-step, we can follow these steps:
Step 1: Understand the Initial Conditions
- The conveyor belt is moving at a speed of vb=5m/s.
- The box has a mass of m=20kg.
- The box is placed on the belt and initially has a velocity of vbox,initial=0m/s relative to the ground.
- The box takes t=0.1s to come to rest with respect to the belt.
Step 2: Determine the Final Velocity of the Box
- After 0.1s, the box comes to rest with respect to the belt, meaning it matches the speed of the belt.
- Therefore, the final velocity of the box relative to the ground is vbox,final=5m/s.
Step 3: Calculate the Acceleration of the Box
- We can use the formula for acceleration:
a=vfinal−vinitialt
- Substituting the values:
a=5m/s−0m/s0.1s=50.1=50m/s2
Step 4: Calculate the Distance Travelled by the Box
- We can use the equation of motion to find the distance travelled:
s=vinitial⋅t+12at2
- Substituting the values:
s=0⋅0.1+12⋅50⋅(0.1)2
s=0+12⋅50⋅0.01=0.25m
Final Answer
The distance travelled by the box during the interval is 0.25m.
---
- The conveyor belt is moving at a speed of vb=5m/s.
- The box has a mass of m=20kg.
- The box is placed on the belt and initially has a velocity of vbox,initial=0m/s relative to the ground.
- The box takes t=0.1s to come to rest with respect to the belt.
- After 0.1s, the box comes to rest with respect to the belt, meaning it matches the speed of the belt.
- Therefore, the final velocity of the box relative to the ground is vbox,final=5m/s.
- We can use the formula for acceleration:
a=vfinal−vinitialt
- Substituting the values:
a=5m/s−0m/s0.1s=50.1=50m/s2
- We can use the equation of motion to find the distance travelled:
s=vinitial⋅t+12at2
- Substituting the values:
s=0⋅0.1+12⋅50⋅(0.1)2
s=0+12⋅50⋅0.01=0.25m
The distance travelled by the box during the interval is 0.25m.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:REVISION EXERCISE (VERY SHORT ANSWER QUESTION)
Explore 40 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:REVISION EXERCISE (FILL IN THE BLANKS)
Explore 10 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:NCERT (MULTIPLE CHOICE QUESTION (TYPE-II))
Explore 5 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:Chapter Practice Test
Explore 15 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Practice Test (For Board Examination)
Explore 12 Videos
Similar Questions
Sand drops from a stationary hopper at the rate of 5kg/s on to a conveyor belt moving with a constant speed of 2m/s. What is the force required to keep the belt moving and what is the power delivered by the motor, moving the belt?
View SolutionA horizontal conveyor belt moves with a constant velocity V.A small block is projected with a velocity of 6m/s on it in a direction opposite to the direction of motion of the belt The block comes to rest relative to the belt in a time 4s.μ=0.3,g=10.m/s2 Find V .
View Solution
Knowledge Check
A conveyor belt is moving at a constant speed of 2m/s . A box is grenty dropped on it. Th ecoefficient of friction between them is μ=0.5 . The distance that the box will move relative to belt before coming to rest on it taking g=10ms−2 is:
A1.2mB0.6mCzeroD0.4mA conveyer belt is moving at a constant speed of 2 ms−1 A box is gently dropped on it. The coefficient of friction between them is μ = 0.5. The distance that the box will move relative to belt before coming to rest on it, taking g=10ms−2, is
A0.4mB1.2 mC0.6mDzeroA long horizontal belt is moving from left to right with a uniform speed 2 m/s. There are two ink marks A and B on the belt 60 m apart. An insect runs on the belt to the fro between A and B such that its speed releatice to belt is constant and equals 4 m/s. When the insect is moving on the belt in the directoin of motion of the belt, its speed as observed by a person standing on ground will be:
A6 m/sB2 m/sC1.5 m/sD4 m/s
A long belt is moving horizontally with a speed of 5kmh−1. A child runs on this belt to and fro with a speed of 9km/h (w.r.t. bett) between his father and mother located 50m apart on the belt. For an observer on a stationalry plateform outsied, what is the
(a) speed of the chils runningin the derection of motion of the belt, (b) speed of thechaild runing opposite to thedirection of the belt, and (c ) time taken by the child in cases (a) and (b) ? Which of theanswers change, if motion is viewed by one of the parents ?gt
View SolutionA conveyor belt is moving with constant speed of 6m/s. A small block is just dropped on it.Coefficient of friction between the two is μ=0.3. Find

(a) The time when relative motion between them will stop
(b) Displacement of block upto that instant (g=10m/s2).
View Solution
A solid sphere of mass m and radius R is gently placed on a conveyer belt moving with constant velocity v0. If coefficient of friction between belt and sphere is 2/7 the distance traveled by the centre of the sphere before it starts pure rolling is
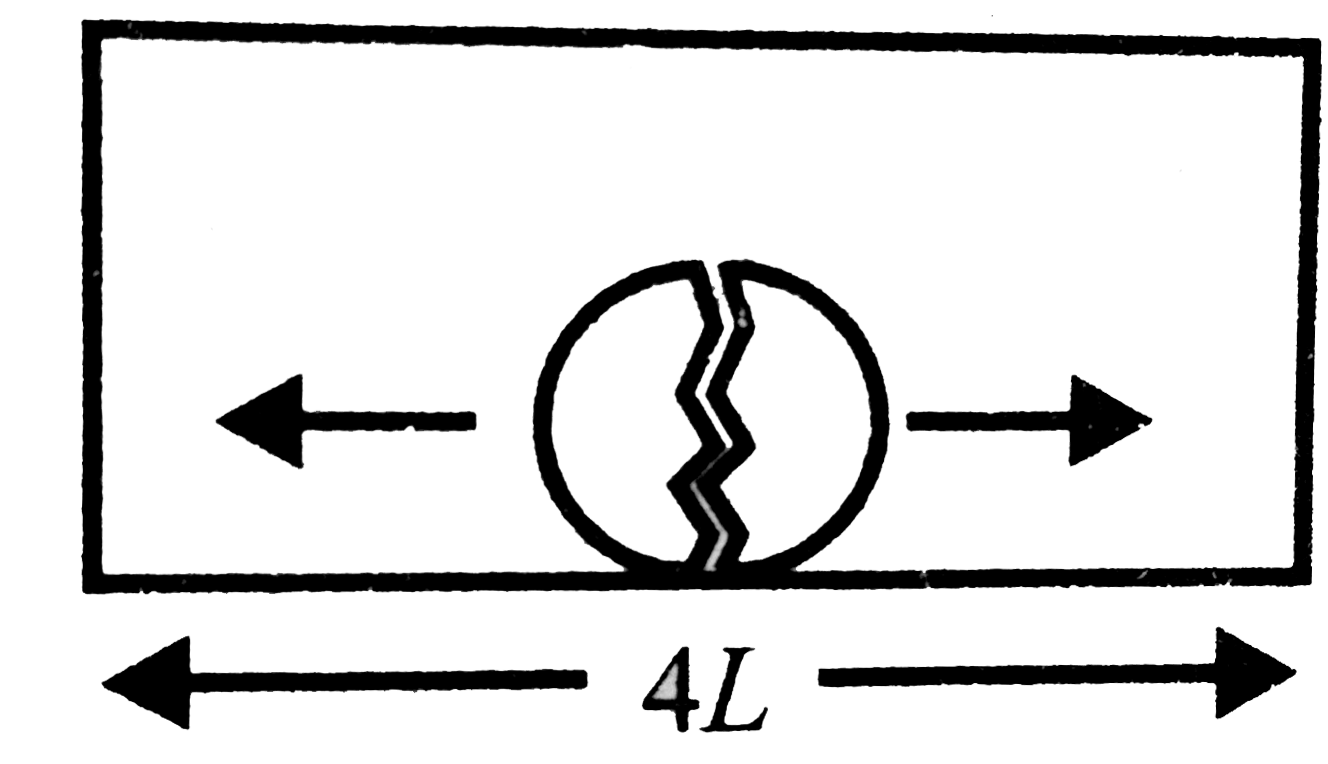
View SolutionA bomb of mass 3m is kept inside a closed box of mass 3m and length 4L at its centre. It explodes in two parts of mass m and 2m. The two parts move in opposite directions and stick to the opposite sides of the walls of box. The box is kept on a smooth horizontal surface. What is the distance moved by the box during this time interval.
View SolutionA 15 N net force is applied for 6.0 s to a 12 kg box initially at rest. What is the speed of the box at the end of the 6.0 s interval?
View Solution
