Let v and a represent instantaneous velocity and acceleration of a particle respectively.
Acceleration a can be zero when velocity v =cancel0
Acceleration a can be nonzero when velocity v=0
Acceleration a can be zero when velocity v=0
Acceleration a must be zero when velocity v=0.
The correct Answer is:a,b,c
To solve the question regarding the relationship between instantaneous velocity (v) and acceleration (a) of a particle, we will analyze each of the given statements one by one.
1. Understanding the Definitions:
- Instantaneous velocity (v) is the velocity of a particle at a specific moment in time.
- Instantaneous acceleration (a) is the rate of change of velocity with respect to time, mathematically expressed as a=dvdt.
2. Analyzing the First Statement:
- Statement: "Acceleration A can be 0 when velocity is not 0."
- Analysis: If a particle is moving with a constant velocity, it means that there is no change in velocity over time. Therefore, the acceleration, which is the change in velocity over time, will be zero.
- Conclusion: This statement is correct.
3. Analyzing the Second Statement:
- Statement: "Acceleration A can be non-zero when velocity is zero."
- Analysis: Consider a ball thrown upwards. At the maximum height, the velocity of the ball is zero (it momentarily stops), but the acceleration due to gravity is still acting downwards (which is non-zero).
- Conclusion: This statement is correct.
4. Analyzing the Third Statement:
- Statement: "Acceleration A can be zero when velocity is equal to zero."
- Analysis: If an object is at rest and not moving, both its velocity and acceleration can be zero. For instance, a stationary object has no movement and hence no acceleration.
- Conclusion: This statement is correct.
5. Analyzing the Fourth Statement:
- Statement: "Acceleration A must be zero when velocity is equal to zero."
- Analysis: While it is possible for both velocity and acceleration to be zero, it is not necessary. For example, an object can have zero velocity at a moment (like at the peak of its throw) while still experiencing acceleration (like gravitational acceleration).
- Conclusion: This statement is incorrect.
Final Summary:
- The first three statements are correct:
1. Acceleration A can be 0 when velocity is not 0. (Correct)
2. Acceleration A can be non-zero when velocity is zero. (Correct)
3. Acceleration A can be zero when velocity is equal to zero. (Correct)
- The fourth statement is incorrect:
4. Acceleration A must be zero when velocity is equal to zero. (Incorrect)
- Instantaneous velocity (v) is the velocity of a particle at a specific moment in time.
- Instantaneous acceleration (a) is the rate of change of velocity with respect to time, mathematically expressed as a=dvdt.
- Statement: "Acceleration A can be 0 when velocity is not 0."
- Analysis: If a particle is moving with a constant velocity, it means that there is no change in velocity over time. Therefore, the acceleration, which is the change in velocity over time, will be zero.
- Conclusion: This statement is correct.
- Statement: "Acceleration A can be non-zero when velocity is zero."
- Analysis: Consider a ball thrown upwards. At the maximum height, the velocity of the ball is zero (it momentarily stops), but the acceleration due to gravity is still acting downwards (which is non-zero).
- Conclusion: This statement is correct.
- Statement: "Acceleration A can be zero when velocity is equal to zero."
- Analysis: If an object is at rest and not moving, both its velocity and acceleration can be zero. For instance, a stationary object has no movement and hence no acceleration.
- Conclusion: This statement is correct.
- Statement: "Acceleration A must be zero when velocity is equal to zero."
- Analysis: While it is possible for both velocity and acceleration to be zero, it is not necessary. For example, an object can have zero velocity at a moment (like at the peak of its throw) while still experiencing acceleration (like gravitational acceleration).
- Conclusion: This statement is incorrect.
- The first three statements are correct:
1. Acceleration A can be 0 when velocity is not 0. (Correct)
2. Acceleration A can be non-zero when velocity is zero. (Correct)
3. Acceleration A can be zero when velocity is equal to zero. (Correct)
- The fourth statement is incorrect:
4. Acceleration A must be zero when velocity is equal to zero. (Incorrect)
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( D.(MULTIPLE CHOICE QUESTIONS))9videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE (ASSERTION REASON)9videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( B.(MULTIPLE CHOICE QUESTIONS))74videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test15videos
MOTION IN A PLANE
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)12videos
OSCILLATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One or More
Let v and a be the instantaneous velocity and acceleration of a particle moving in a plane. Then rate of change of speed dvdt of the particle is equal to
A|a|Bv.avCthe component of a parallel to vDthe component of a perpendicular to v - Question 2 - Select One
The phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is
A0.5πBπC0.707πDzero - Question 3 - Select One
The phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is
A0.5πBπC0.707πDzero
The phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is:
View SolutionThe phase difference between the instantaneous Velocity and acceleration of a particle executing simple harmonic motion is
View SolutionFor a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
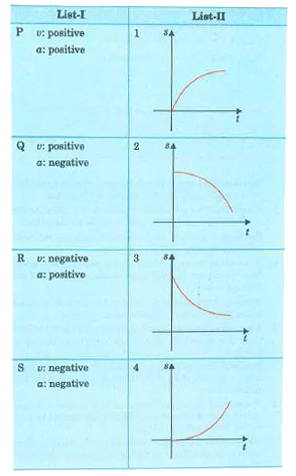 View Solution
View SolutionThe graph between instantaneous velocity and acceleration of a particle performing S.H.M. is
View SolutionThe graph between instantaneous velocity and acceleration of a particle performing S.H.M. with a period of 6.28 s is
View Solution

