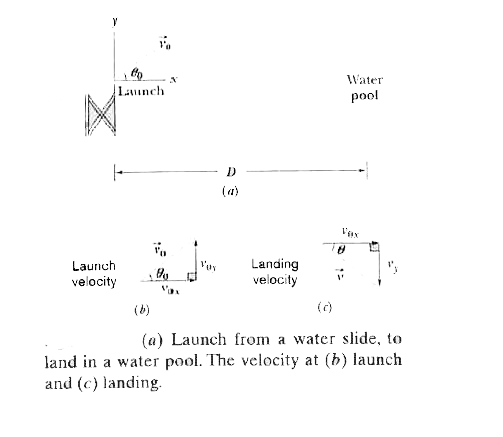
One of the most dramatic videos on the web (but entirely fictitious) supposedly shows a man sliding along a long water slide and then being launched into the air to land in a water pool. Let's attach some reasonable numbers to such a flight to calculate the velocity with which the man would have hit the water. Figure a indicates the launch and landing sites and includes a superimposed coordinate system with its origin conveniently located at the launch site. From the video we take the horizontal flight distance as D = 20.0 m, the flight time as t = 2.50 s, and the launch angle as θ0=40.0∘ . Find the magnitude of the velocity at launch and at landing.
Text Solution
(1) For projectile motion, we can apply the equations for constant acceleration along the horizontal and vertical axes separately. (2) Throughout the flight, the Vertical acceleration is ay=−g=−9.8m/s2 and the horizontal acceleration is ax = 0.
In most projectile problems, the initial challenge is to figure out where to start. There is nothing wrong with trying out various equations, to see if we can somehow get to the velocities. But here is a clue. Because we are going to apply the constant acceleration equations separately to the x and y motions, we should find the horizontal and vertical components of the velocities at launch and at landing. For each site, we can then combine the velocity components to get the velocity. Because we know the horizontal displacement D=20.0 m, let.s start with the horizontal motion. Since ax = 0, we know that the horizontal velocity component vx is constant during the flight and thus is always equal to the horizontal component v0 , at launch . we can relate that component , the displacement x−x0 and the flight time t = 2.50 s with eq.
x−x0=v0t+12at2
substituting ax=0, this becomes eq. with x−x0=D we the write
20m=v0(2.0s)+12(0)(2.50s)2
v0x=8.00m/s
That is a component of the launch velocity , but we need the magnitude of the full vector ,
where the component form the legs of a right triangle and the vector forms the hypotenuse . we can them apply a trig definition to find the magnitude of the full velocity at launch :
cosθ0=v0xv0
v0=v0xcosθ0=8.00m/scos40∘
= 10.44 m//s ~~ 10.4 m//s
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - CHECKPOINT3videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS50videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Animals living on a land and in water
AAmbiguousBAmphibianCAmorphousDAmbivalent - Question 2 - Select One
Reptile living on water as well as on land is
APythonBSphenodonCTurtle/TortoiseDFrog. - Question 3 - Select One
The narrow area of contact between land, air and water is called
ALithosphereBBiosphereCAtmosphereDHydrosphere
Reptile living on water as well as on land is
View SolutionMammals occur on land, air and water. It is
View SolutionLand slide, locust, Riot, flood and earthquake.
View SolutionA child slides without friction from a height h along a curved water slide (figure). She is launched from a height h/5 into the pool. Determine her maximum airbone height y in terms of h and θ.
 View Solution
View SolutionA child slides without friction from a height h along a curved water slide (figure). She is launched from a height h/5 into the pool. Determine her maximum airbone height y in terms of h and θ.
 View Solution
View Solution

