An electric spark jumps along a straight line of length L = 10 m, emitting a pulse of sound that travels radially outward from the spark. (The spark is said to be a line source of sound.) The power of this acoustic emission is $P = 1.6 \times 10^{4}$ W. (a) What is the intensity I of the sound when it reaches a distance r = 12 m from the spark? (b) At what time rate $P_{A}$ is sound energy intercepted by an acoustic detector of area $A_{d} = 2.0 c m^{2}$ ?, aimed at the spark and located a distance r = 12 m from the spark?

Text Solution

Verified by Experts

(1) Let us center an imaginary cylinder of radius r = 12 m and length L = 10 m (open at both ends) on the spark, as shown in Fig. Then the intensity I at the cylindrical surface is the ratio P/A, where P is the time rate at which sound energy passes through the surface and A is the surface area. (2) We assume that the principle of conservation of energy applies to the sound energy. This means that the rate P at which energy is transferred

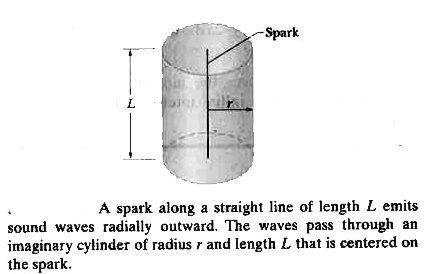
through the cylinder must equal the rate $P_{s}$ at which energy is emitted by the source.
Putting these ideas together and noting that the area of the cylindrical surface is $A = 2 π r L$ ,we have
$I = \frac{P}{A} = \frac{P_{s}}{2 π r L}$
This tells us that the intensity of the sound from a line source decreases with distance r (and not with the square of distance r as for a point source). Substituting the given data, we find
$I = \frac{1.6 \times 10^{4} W}{2 π (12 m) (10 m)}$
$= 21.2 W / m^{2} \approx 21 W / m^{2}$
(b) We know that the intensity of sound at the detector is the ratio of the energy transfer rate $P_{d}$ there to the detector.s area $A_{d}$ :
$I = \frac{P_{d}}{A_{d}}$
We can imagine that the detector lies on the cylindrical surface of (a). Then the sound intensity at the detector is the intensity I( = $21.2 W / m^{2}$ ) at the cylindrical surface. Solving Eq. for $P_{d}$ gives us
$P_{d} = (21.2 W / m^{2}) (2.0 \times 10^{- 4} m^{2}) = 4.2 m W$

Updated on:21/07/2023

Intensity of sound at a point is its distance from the source
Adirectly proportional to
Binversely proportional to
Cdirectly proportional to square of
Dinversely proportional to square of
The sound intensity is $0.008 W / m^{2}$ at a distance of 10 m from an isotropic point source of sound. The power of the source is
A $2.5 W$
B $0.8 W$
C $8 W$
D $10 W$
The intensity of sound from a radio at a distance of 2 metres from its speaker is $1 \times 10^{- 2} μ W / m^{2}$ . The intensity at a distance of 10 meters would be
A $0.2 \times 10^{- 2} μ W / m^{2}$
B $1 \times 10^{- 2} μ W / m^{2}$
C $4 \times 10^{- 4} μ W / m^{2}$
D $5 \times 10^{- 2} μ W / m^{2}$