Question

In Fig. , two point sources $S_1$ and $S_2$ which are in phase and separated by distance $D=1.5\lambda$ , emit identical sound waves of wavelength $\lambda$.
(a) What is the path length difference of the waves from $S_1$ and $S_2$ at point $P_1$, which lies on the perpendicular bisector of distance D, at a distance greater than D from the sources ? (That is, what is the difference in the distance from source $S_1$ to point $P_1$ and the distance from source $S_2$ to $P_1$?) What type of interference occurs at $P_1$ ?
(b) What are the path length difference and type of interference at point $P_2$ in fig.
(c ) Figure shows a circle with a radius much greater than D, centered on the midpoint between sources $S_1$ and $S_2$. What is the number of points N around this circle at which the interference is fully constructive? (That is, at how many points do the waves arrive exactly in phase?)

Explanation

(a) Because the waves travel identical distances to reach `P_1` their path length difference is `Delta L = theta `
From Eq., this means that the waves undergo fully constructive interference at `P_1` because they start in phase at the sources and reach `P_1` in phase.
(b) The wave from `S_1` travels the extra distance D(=1.5`lamda`) to reach `P_2` Thus, the path length difference is
`DeltaL = 1.5 lamda`
this means that the waves are exactly out of phase at `P_2` and undergo fully destructive interference there.

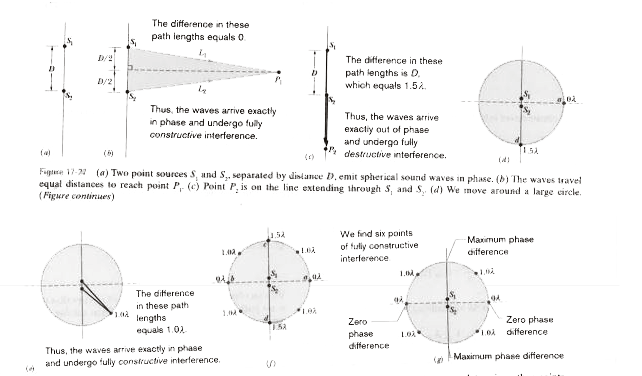
(c )Starting at point a, let.s move clockwise along the circle to point d. As we move, path length difference `DeltaL` increases and so the type of interference changes. From (a), we know that is `Delta L = 0 lamda` at point a. From (b), we know that `Delta L = 1.5 lamda ` at point d. Thus, there must be one point between a and d at which `Delta L = lamda `
From Eq. , fully constructive interference occurs at that point. Also, there can be no other point along the way from point a to point d at which fully constructive interference occurs, because there is no other integer than 1 between 0 at point a and 1.5 at point d. We can now use symmetry to locate other points of fully constructive or destructive interference. Symmetry about line cd gives us point b, at which `Delta L = 0lamda ` . Also, there are three more points at which `Delta L = lamda` . In all we have
N = 6.