What is the intensity at radial distances (a) 2.50 m and (b) 6.00 m from an isotropic point source of sound that emits energy at the rate 12.0 W, assuming no energy absorption by the surrounding air?
To solve the problem of finding the intensity at radial distances of 2.50 m and 6.00 m from an isotropic point source of sound emitting energy at a rate of 12.0 W, we will follow these steps:
Step 1: Understand the concept of intensity
Intensity (I) is defined as the power (P) per unit area (A). For a point source emitting sound isotropically, the sound spreads out uniformly in all directions, forming a sphere around the source.
Step 2: Write the formula for intensity
The formula for intensity is given by:
I=PA
where:
- P is the power of the source (in watts),
- A is the area over which the power is distributed.
Step 3: Calculate the area of the spherical surface
The area of a sphere is calculated using the formula:
A=4πR2
where R is the radius (the radial distance from the source).
Step 4: Calculate intensity at 2.50 m
1. Determine the radius: For the first part, R=2.50m.
2. Calculate the area:
A=4π(2.50)2=4π(6.25)=25πm2
3. Substitute into the intensity formula:
I=12.0W25π≈12.078.54≈0.153W/m2
Step 5: Calculate intensity at 6.00 m
1. Determine the radius: For the second part, R=6.00m.
2. Calculate the area:
A=4π(6.00)2=4π(36)=144πm2
3. Substitute into the intensity formula:
I=12.0W144π≈12.0452.39≈0.0265W/m2
Final Answers:
- (a) The intensity at 2.50 m is approximately 0.153W/m2.
- (b) The intensity at 6.00 m is approximately 0.0265W/m2.
Intensity (I) is defined as the power (P) per unit area (A). For a point source emitting sound isotropically, the sound spreads out uniformly in all directions, forming a sphere around the source.
The formula for intensity is given by:
I=PA
where:
- P is the power of the source (in watts),
- A is the area over which the power is distributed.
The area of a sphere is calculated using the formula:
A=4πR2
where R is the radius (the radial distance from the source).
1. Determine the radius: For the first part, R=2.50m.
2. Calculate the area:
A=4π(2.50)2=4π(6.25)=25πm2
3. Substitute into the intensity formula:
I=12.0W25π≈12.078.54≈0.153W/m2
1. Determine the radius: For the second part, R=6.00m.
2. Calculate the area:
A=4π(6.00)2=4π(36)=144πm2
3. Substitute into the intensity formula:
I=12.0W144π≈12.0452.39≈0.0265W/m2
- (a) The intensity at 2.50 m is approximately 0.153W/m2.
- (b) The intensity at 6.00 m is approximately 0.0265W/m2.
Topper's Solved these Questions
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
35 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
6 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - CHECKPOINTS
4 Videos
- VECTORS BOOK - RESNICK AND HALLIDAYCHAPTER - VECTORS EXERCISE - PRACTICE QUESTIONS
39 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
A potassium foil is a distance r=3.5m from an isotropic light source that emits energy at the rate P=1.5W. The work function F of potassium is 2.2 eV. Suppose that the energy transported by the incident light were transferred to the target foil continuously and smoothly (that is, if classical physics prevailed instead of quantum physics). How long would it take for the foil to absorb enough energy to eject and electron? Assume that the foil totally absorbs all the energy reaching it can that the to - be-ejected electron collects energy from a circular patch of the foil whose radius is 5.0×10−11m, about that of a typical atom.
View SolutionFind the damping coefficient v of a sound wave if at distances r1=10m and r2=20m from a point isotropic source of sound the sound wave intensity values differ by a factor η=4.5.
View Solution
Knowledge Check
The sound intensity is 0.008W/m2 at a distance of 10 m from an isotropic point source of sound. The power of the source is
A2.5WB0.8WC8WD10WA person is standing at a distance D from an isotropic point source of sound He walks 50.0 m towards the source and observes that the intensity of the sound has doubled. His initial distance D from the source is
A50√2mB50√2√2−1mC50√2−1mD100√2mAt a distance of 5.0 m from a point sound source, the sound intensity level is 110 dB. At what distance is the intensity level 95 dB?
A5.0 mB14 mC7.1 mD28 m
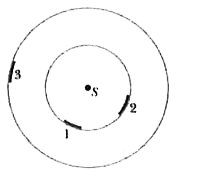
The figure indicates three small patches 1, 2, and 3 that lie on the surfaces of two imaginary spheres, the spheres are centered on an isotropic point source S of sound. The rates at which energy is transmitted through the three patches by the sound waves are equal. Rank the patches according to (a) the intensity of the sound on them and (b) their area, greatest first.
View SolutionLoudness of sound from an isotropic point source at a distace of 70cm is 20dB. What is the distance (in m) at which it is not heard.
View SolutionAt a distance r0=20m form an isotropic point source of sound the loudness level is L0=30dB. Neglicting the damping of the sound wave, find : (a) the loudness level at a distacne r=10m form the source, (b) the distance form the source at which sound is not heard.
View SolutionCalculate the intensity of illumination at a distance of 0.5m from a source of light of power 200 candela assuming normal incidence.
View SolutionA source of sound operates at 2.0 kHz, 20 W emitting sound uniformly in all direction. The speed of sound in air is 340ms−1 at a distance of air is 1.2kgm−3 (a) What is the intensity at a distance of 6.0 m from the source ? (b) What will be the pressure amplitude at this point ? (c ) What will be the displacement amplitude at this point ?
View Solution
