Figure shows the output from a pressure monitor mounted at a point along the path taken by a sound wave of a single frequency traveling at 343 m/s through air with a uniform density of 1.21kg/m3. The vertical axis scale is set by Δp=5.0mPa . If the displacement function of the wave is s(.x, t) = smcos(kx−ωt) , what are (a) sm(b) k, and (c) ω? The air is then cooled so that its density is 1.35 kg/m and the speed of a sound wave through it is 320 m/s. The sound source again emits the sound wave at the same frequency and same pressure amplitude. What now are (d)sm,(c)k,and(f)ω?
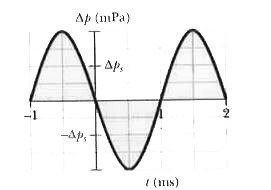
(a)343m/s,(b)9.2rad/m(c)3142rad/s≈3.1×103rad/s,(d)7.4nm,(e)9.8rad/m,(f)3142rad/s≈3.1×103rad/s
Topper's Solved these Questions
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
35 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
6 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - CHECKPOINTS
4 Videos
- VECTORS BOOK - RESNICK AND HALLIDAYCHAPTER - VECTORS EXERCISE - PRACTICE QUESTIONS
39 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
Knowledge Check
The graph shows a wave at t=0 travelling to the right with a velocity of 4m/s. The equation that best represents the wave is
 Ay(x,t)=2sin(πx/4−πt)metresBy(x,t)=2sin(16πx−8πt)metresCy(x,t)=2sin(πx/4+πt)metresD4 sin(pix//4-pit) metres
Ay(x,t)=2sin(πx/4−πt)metresBy(x,t)=2sin(16πx−8πt)metresCy(x,t)=2sin(πx/4+πt)metresD4 sin(pix//4-pit) metresSounds waves travel at 350m/s through a warm air and at 3500m/s through brass. The wavelength of a 700Hz. Acoustic wave as it enters brass from warm air
ADecreases by a factor 20BDecreases by a factor 10CIncreases by a factor 20DIncreases by a factor 10The speed of sound waves in air is 340 m/s and 5600 m/s through steel. The wavelength of a 1000 Hz acoustic wave travelling from air to steel will
Adecrease by a factor 15Bincrease by a factor 20Cdecrease by a factor 10Dincrease by a factor 16.5
The given graph shows the displacement versus time relation for a sound wave travelling with velocity of 1500 m s−1. Find the wavelength of the sound wave.
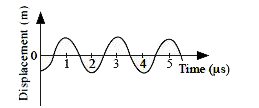
View SolutionThe graph shows a wave at t=0 travelling to the right with a velocity of 4m/s. The equation that best represents the wave is

View SolutionA sound wave travels at a speed of 340 m/s. It its wavelength is 2 cm, what is the frequency of the wave ? Will it be in the audible range ?
View SolutionA sound wave travels with a speed of 330ms−1 in air. If the wavelength of the wave is 330 cm, then the frequency of the wave is ______
View SolutionPlane harmonic waves of frequency 500 Hz are produced in air with displacement amplitude of 10μm. Given that density of air is 1.29kgm3 and speed of sound in air is 340ms. Then
View Solution
