Vibrations with frequency 6.00×102 Hz are established on a 1.33 m length of string that is clamed at both ends. The speed of waves on the string is 4.0×102m/s
How many antinodes are contained in the resulting standing wave pattern?
2
4
3
5
The correct Answer is:B
To find the number of antinodes in the standing wave pattern formed on a string clamped at both ends, we can follow these steps:
Step 1: Understand the relationship between harmonics and standing waves
For a string clamped at both ends, the standing wave pattern consists of nodes and antinodes. The number of antinodes is related to the harmonic of the wave. The nth harmonic has n antinodes and (n + 1) nodes.
Step 2: Use the formula for the wavelength in terms of the harmonic
The relationship between the length of the string (L), the wavelength (λ), and the harmonic number (n) is given by:
L=nλ2
This means that the length of the string is equal to n half-wavelengths.
Step 3: Relate wavelength to wave speed and frequency
The wavelength can also be expressed in terms of wave speed (v) and frequency (f):
λ=vf
Step 4: Substitute the expression for wavelength into the length equation
Substituting the expression for λ into the length equation gives:
L=n2⋅vf
Step 5: Rearrange to find n
Rearranging the equation to solve for n gives:
n=2Lfv
Step 6: Substitute the known values
Given:
- Length of the string, L=1.33m
- Frequency, f=6.00×102Hz=600Hz
- Wave speed, v=4.0×102m/s=400m/s
Now, substituting these values into the equation:
n=2×1.33×600400
Step 7: Calculate n
Calculating the above expression:
n=2×1.33×600400=1596400=3.99≈4
Step 8: Determine the number of antinodes
Since we found n=4, the number of antinodes in the standing wave pattern is equal to n:
Number of antinodes=n=4
Final Answer
Thus, the number of antinodes contained in the resulting standing wave pattern is 4.
---
For a string clamped at both ends, the standing wave pattern consists of nodes and antinodes. The number of antinodes is related to the harmonic of the wave. The nth harmonic has n antinodes and (n + 1) nodes.
The relationship between the length of the string (L), the wavelength (λ), and the harmonic number (n) is given by:
L=nλ2
This means that the length of the string is equal to n half-wavelengths.
The wavelength can also be expressed in terms of wave speed (v) and frequency (f):
λ=vf
Substituting the expression for λ into the length equation gives:
L=n2⋅vf
Rearranging the equation to solve for n gives:
n=2Lfv
Given:
- Length of the string, L=1.33m
- Frequency, f=6.00×102Hz=600Hz
- Wave speed, v=4.0×102m/s=400m/s
n=2×1.33×600400
Calculating the above expression:
n=2×1.33×600400=1596400=3.99≈4
Since we found n=4, the number of antinodes in the standing wave pattern is equal to n:
Number of antinodes=n=4
Thus, the number of antinodes contained in the resulting standing wave pattern is 4.
Topper's Solved these Questions
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (MATRIX MATCH)
4 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
5 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
6 Videos
- VECTORS BOOK - RESNICK AND HALLIDAYCHAPTER - VECTORS EXERCISE - PRACTICE QUESTIONS
39 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
The vibrations from an 800 Hz tuning fork set up standing waves in a string clamped at both ends. The wave speed in the string is known to be 400m/s for the tension used. The standing wave is observed to have four antinodes. How long is the string?
View Solution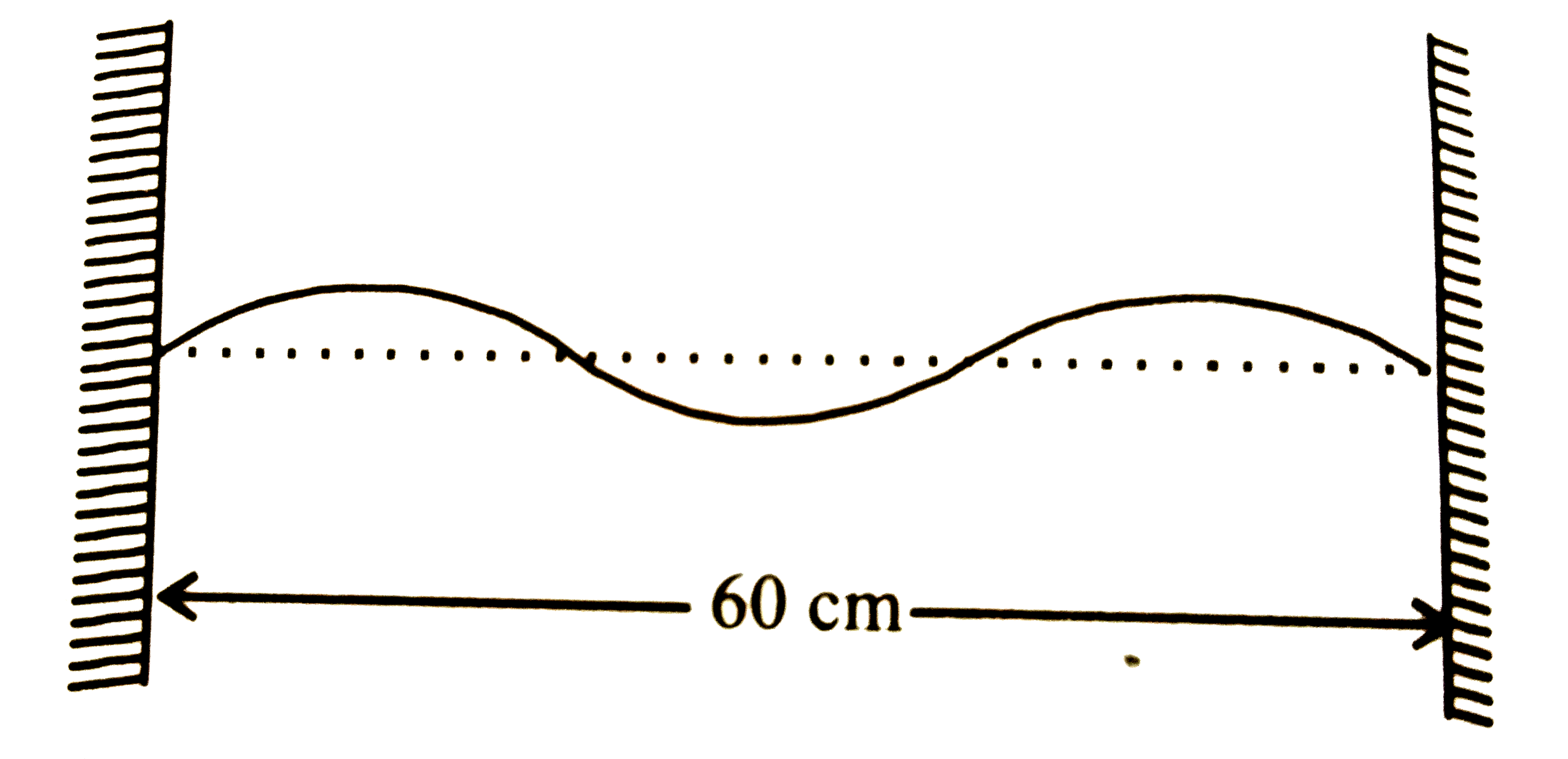
The standing wave pattern along a string of length 60 cm is shown in the above diagram. If the speed of the transverse waves on this string is 300 m/s, in which one of the following modes is the string vibrating?
View Solution
Knowledge Check
Vibrations with frequency 6.00×102 Hz are established on a 1.33 m length of string that is clamed at both ends. The speed of waves on the string is 4.0×102m/s
How far from either end of the string does the first node occur?A0.17mB0.49 mC0.33mD0.66 mA 12 m long vibrating string has the speed of wave 48 m/s . To what frequency it will increase .
A2 cpsB4 cpsC6 cpsDAll of theseA string is stretched by a force of 40 newton. The mass of 10 m length of this string is 0.01 kg. the speed of transverse waves in this string will be
A400m/sB40 m/sC200 m/sD80 m/s
A string 1m long is drawn by a 300 Hz vibrator attached to its end. The string vibrates in three segments. The speed of transverse waves in the string is equal to
View SolutionA 4.00-m long string, clamped at both ends, vibrates at 2.00×102 Hz. If the string resonates in six segments, what is the speed of transverse waves on the string?
View SolutionOne end of a taut string of length 3m along the x-axis is fixed at x=0. The speed of the waves in the string is 100ms−1. The other end of the string is vibrating in the y-direction so that stationary waves are set up in the string. The possible wavelength(s) of these sationary waves is (are)
View SolutionThe frequency of a wave light is 1.0×106sec−1. The wave length for this wave is
View SolutionThe velocity of waves in a string fixed at both ends is 3 m/s. The string forms standing waves with nodes 6 cm apart. The frequency of vibration of the string is
View Solution
