Figure shows a cross-section of a long ribbon of width ω that is carrying a uniformly distributed total current i into the page. Calculate the magnitude and direction of the magnetic field B at a point P in the plane of the ribbon at a distance d from its edge.

The correct Answer is:(23.5pT)ˆj
Step by step video, text & image solution for Figure shows a cross-section of a long ribbon of width omega that is carrying a uniformly distributed total current i into the page. Calculate the magnitude and direction of the magnetic field B at a point P in the plane of the ribbon at a distance d from its edge. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Single Correct)36videos
MAGNETIC FIELDS DUE TO CURRENTS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (More Than one correct choice )12videos
MAGNETIC FIELDS DUE TO CURRENTS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Check point4videos
MAGNETIC FIELDS DUE TO CURRENTS
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Integer Type)6videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )7videos
MAGNETIC FORCE
Similar Questions
The figure shows the cross-section of a long cylindrical conductor of radius a carrying a uniformly distributed current i. The magnetic field due to current at P is :
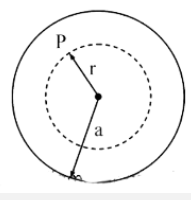 View Solution
View SolutionA square loop of wire, edge length a, carries a current i. Compute the magnitude of the magnetic field produced at a point on the axis of the loop at a distance x from the centre.
View Solution
Knowledge Check
- Question 1 - Select One
A long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.
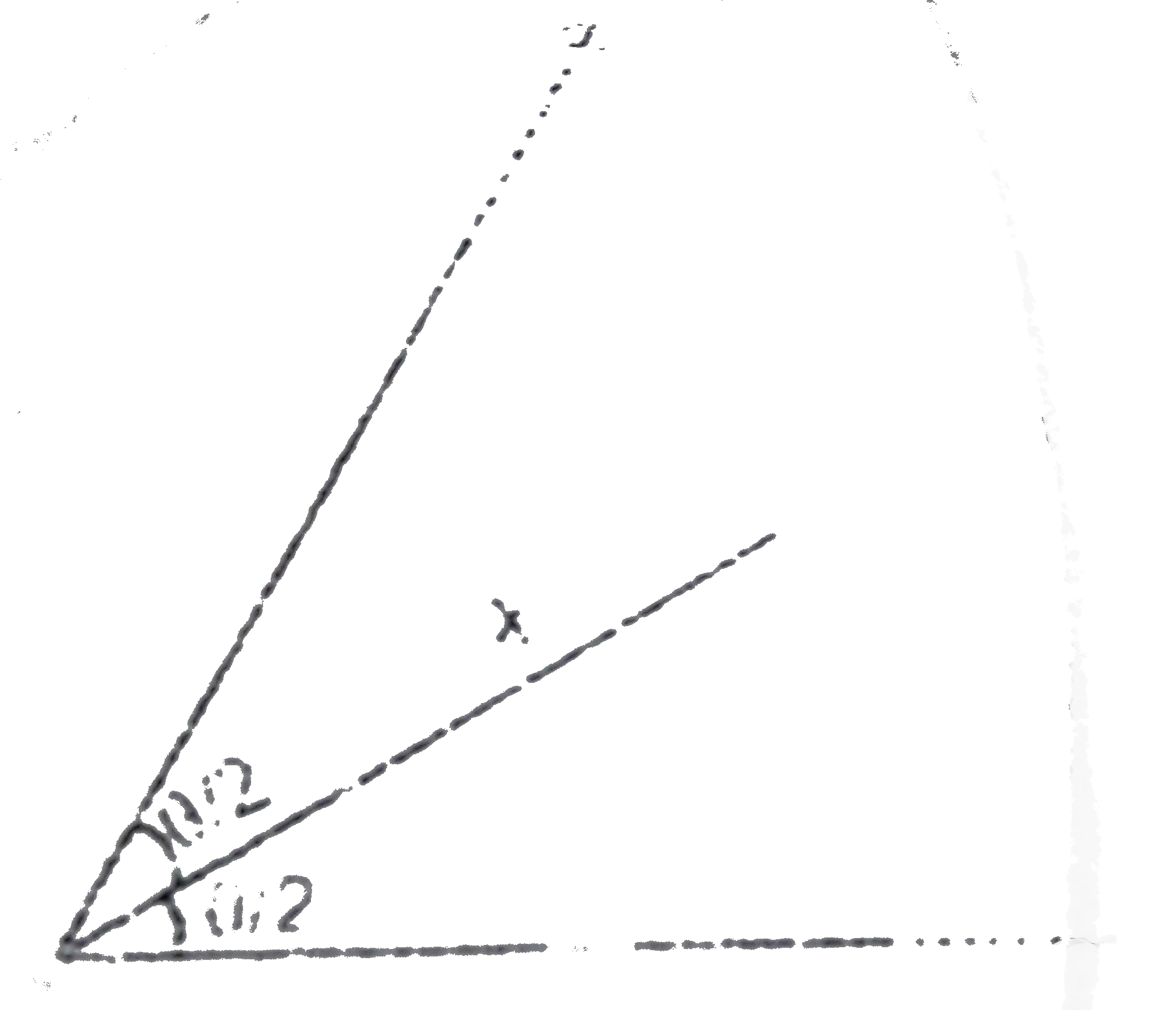 Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙
Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙ - Question 2 - Select One
Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
Aμ0idπ(d2+x2)Bμ0ixπ(d2−x2)Cμ0ix(d2+x2)Dμ0id(d2+x2) - Question 3 - Select One
Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
Aμ0idπ(d2+x2)Bμ0ixπ(d2−x2)Cμ0ix(d2+x2)Dμ0id(d2+x2)
In the figure are shown two long parallel current carrying wires I and II. Find the magnitudes and directions of the magnetic field induction at the point P, Q and R in the plane of paper.
 View Solution
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be
 View Solution
View SolutionA long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
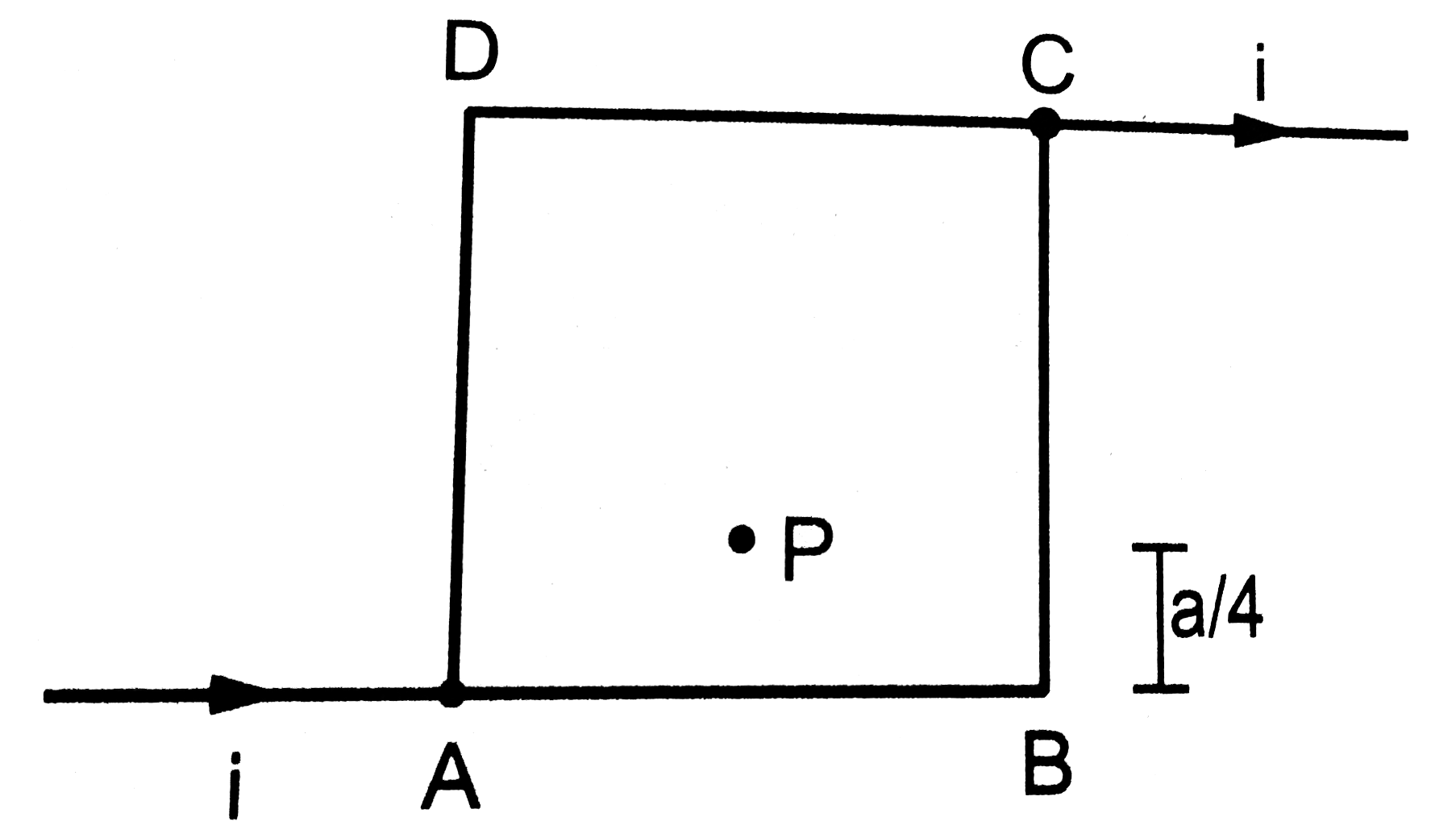 View Solution
View SolutionIn Fig. a larger metal sheet of width w carries a current I(uniformly distributed in its width w). Find the magnetic field at point P which lies on the plane of the sheet.

 View Solution
View Solution
