Sparkle in the diamond
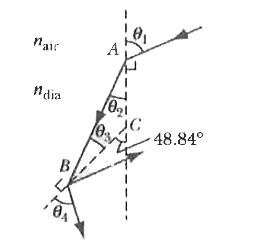
The purpose of a diamond is, of course, to sparkle . Part of the art of cutting a diamond is to ensure that all the light entering through the top face or side facets leaves through those surfaces, to participate in the sparkle. Figure 34-18 shows part of a cross-sectional slice through a brilliant-cut diamond, with a ray entering at point A on the top face. In this type of cut, the top and bottom surfaces have normal lines that intersect at the indicated ${48.84}^{\circ}$ . At point B, at least part of the light reflects and leaves the diamond properly , but part could refract and thus leak out of the diamond. Consider a light ray incident at angle $θ_{1} = 40^{\circ}$ at A. Does light leak at B if air $(n_{4} = 1.00)$ lies next to the bottom surface ? Does light leak if greasy grime $(n_{4} = 1.63)$ coats the surface? The index of refraction of diamond is $n_{d \in} = 2.419$ .

Text Solution

Verified by Experts

When light reaches the interface between two materials with different indexes of refraction (call them $n_{1}$ and $n_{2}$ ), part of all of the light is reflected. The reflection is total if (1) the incident light is in the material with the higher index of refraction $(n_{1} > n_{2})$ and $(2)$ the incident angle exceeds a critical value given by Eq. 34-10
$θ = {sin}^{- 1} (\frac{n_{1}}{n_{2}})$
If those two conditions are not met, part of the light is refracted across the interface according to Snell.s law.
Case 1 : Clean diamond
We need to follow the light from point A to point B to see if it can leak at point B. The light incident at point A is in the material (air $n_{1} = 1.00$ ) with a lower index of refraction than the material on the other side of the interface (diamond $n_{d i a} = 2.419$ ). Thus, some of the light is refracted across the interface (the reflected portion is not shown in Fig. 34-18), and we find the angle of refraction from Snell.s law
Calculation :
$θ_{2} = {sin}^{- 1} (\frac{{sin 40}^{\circ}}{2.419}) = {15.41}^{\circ}$
Now, note that the given angle of ${48.84}^{\circ}$ at point C is an exteriror angle of triangle ABC and thus (from Appendix E), we can write
$θ_{3} + θ_{2} = {48.84}^{\circ}$
or $θ_{3} = {49.84}^{\circ} - θ_{2} = {33.43}^{\circ}$
This is the angle of incidence of the ray at point B. Now the incident light is in the material (diamond) with the greater index of refraction than the material (air) on the other side of the interface. However, if we apply Snell.s law at point B, we find no answer. The reason is that the light is incident at an angle greater than the critical value of
$θ_{c} {sin}^{- 1} (\frac{n_{4}}{n_{d i a}}) = {sin}^{- 1} (\frac{1.00}{2.419}) = {24.4}^{\circ}$
Thus, all the light reaching B reflects and none leaks out in the air.
Case 2 : Grimy diamond
We again follow the light from A to B, with the only difference lying in the last two calculations.
Now at B, the material on the other side of the interface is grime with an index $n_{4} = 1.63$ . The incident light is again in the material with the greater index, but now the critical angle is
$θ_{c} = {sin}^{- 1} (\frac{n_{4}}{n_{d i a}}) = {sin}^{- 1} (\frac{1.63}{2.419}) = {42.4}^{\circ}$
Therefore, the incident angle $n_{3} = {33.43}^{\circ}$ is less than the critical angle and light leaks through the bottom of the diamond.
From Snell.s law, the angle of refraction is
$θ_{4} = {sin}^{- 1} (\frac{2.419}{1.63} {sin 33.43}^{\circ}) = {54.8}^{\circ}$
Learn Thus, to keep a diamond sparkling, clean both the top and bottom surfaces.

Updated on:21/07/2023