Formation of image by a combination of converging and a diverging lens
Find the location of the final image after all the refrections in Fig. 34-41. The radius of both the plano-convex lens and plano-concave lens is 10cm and refrective index is 1.5.
Here again we are seeing an example of multiple events. The image of plano-convex lens will act as an object for the plano-concave lens. But to get there, we need to find the focal length of the lens first.
Calculation : Focal length of the plano-convex lens is
1f=(1.5−1)(1+10−1∞)=120
Focal length of plano-concave lens is
1f=(1.5−1)(1∞−1+10)=−120
Since parallel beam is incident on the lens, its image from plano-convex lens will be formed at +20cm from it (at the focus) and will act as an object for the plano-concave Since the two lenses are at a distance of 10cm from each other therefore for the next lens u=+10cm. Hence
v=ufu+f=10×−2010−20=20cm
Learn : We can see that a diverging lens is forming a real image. This is because the object for it is virtual and is between pole and object focus.
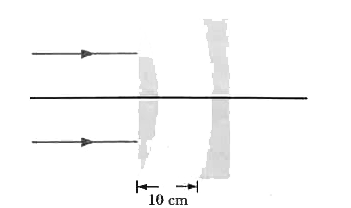
Topper's Solved these Questions
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Check point
6 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Problems
44 Videos
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
4 Videos
Similar Questions
Find the radius of curvature of the convex surface of a plano-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View SolutionFind the radius of curvature of the convex surface of a plano-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View Solution
Knowledge Check
Find the focal length of plano-convex lens of material having refractive index of 1.5. Radius of curvature of convex surface is 10 cm.
 A20 cmB30cmC50 cmD40 cm
A20 cmB30cmC50 cmD40 cmThe radius of curvature of the convex surface of a thin plano-convex lens is 15 cm and the refractive index of its material is 1.6. The power of the lens is
A+1DB−2DC+3DD+4DThe radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
A30cmB50cmC20cmD40cm
Find the refractive index of the material of a plano-convex lens, if the radius of curvature of the convex surface is 20 cm and focal length of the lens is 60 cm?
View SolutionFind the refractive index of the material of a plano-convex lens, if the radius of curvature of the convex surface is 20 cm and focal length of the lens is 60 cm?
View SolutionWhat is the refractive index of material of a plano-convex lens , if the radius of curvature of the convex surface is 10 cm and focal length of the lens is 30 cm ?
View SolutionA lens produces a magnification of -0.5. Is this a converging or diverging lens? If the focal length of the lens is 6 cm, draw a ray diagram showing the image formation in this case.
View SolutionWhat is the refractive index of material of a plano-convex lens , if the radius of curvature of the convex surface is 10 cm and focal length of the lens is 30 cm ?
View Solution
