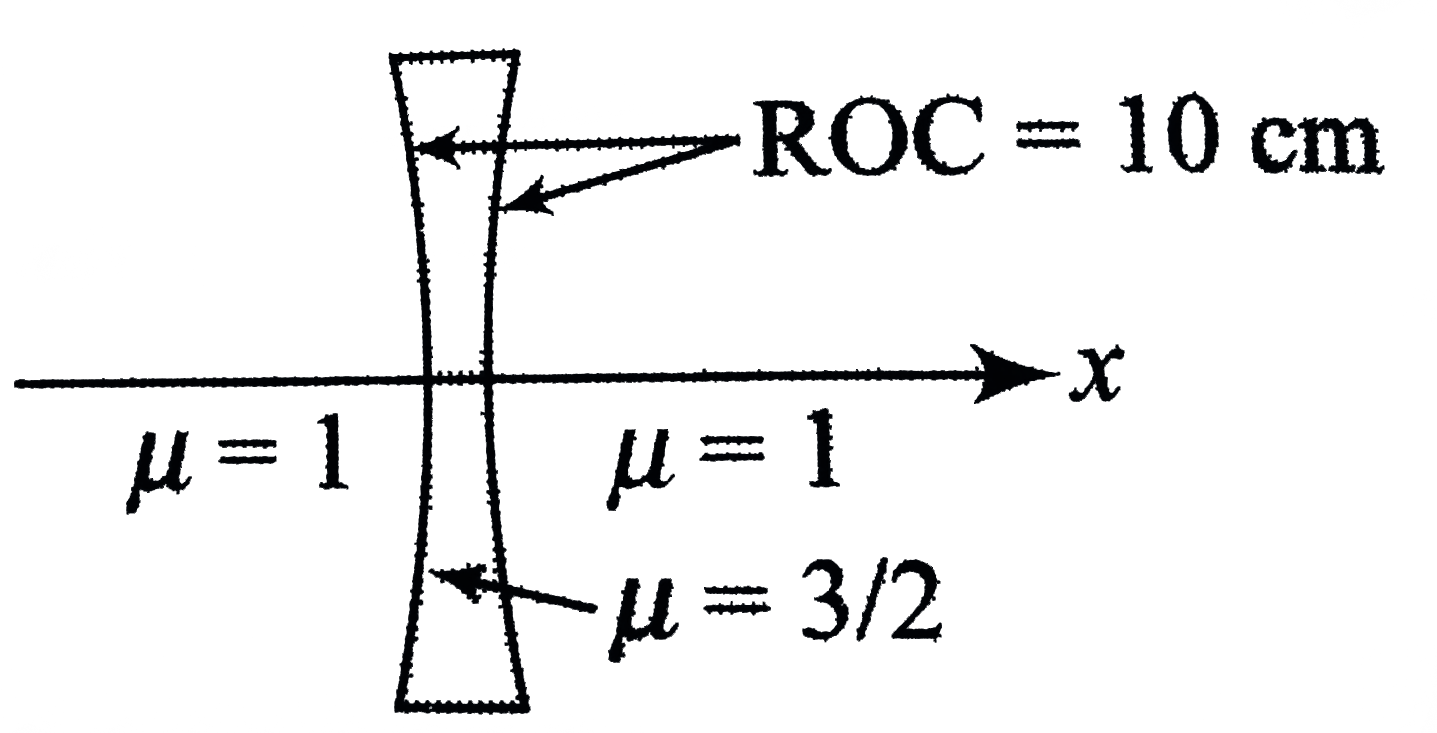Finding equivalent focal length
Two equiconcave lens of focal length -20cm each having a refractive index of 1.50 are kept together and the space between them is filled with water as shown in Fig. 34-49. Find the equivalent focal length of the arrangement thus formed.
Text Solution
(1) Here we can imagine a thin layer of air in between lens and water at both the surfaces (Fig. 34-50). This will give us two concave lenses combined with a convex lens of water. This thin layer of air will not affect the formation of image but rather will simplify the calculations a lot.
(2) First let us find the radius of curvature of the lens because this will needed to find the focal length of the convex lens formed by water in between .
Calculations :
1−20=(1.5−1)(1−R−1R)
R=20cm
So, the focal length of water convex lens (in Fig. 34-50) is
1f=(43−1)(120−1−20)
f=30cm
Note here carefully that we are taking the focal length of the water lens in air because when we are using the focal length of the concave lens, we are assuming that there is air on both the sides.
1f=1f1+1f2+1f1
1f=1−20+130+1−20
f=−15cm
Learn : Similarly, if a lens is cut into two parts, the focal length of the two parts are given by
1f=1f1+1f2
where f is the focal length of the original lens and f1 and f2 are focal lengths of the two cut parts. The interesting situation is that if we join these lenses back, we will get back the original lens. We have studied previously that the focal length of the lens does not depend on the side facing the light. So, the focal length of all the following four arrangements (Figs. 34-51a-d) will be the same.

|
Topper's Solved these Questions
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Check point
6 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Problems
44 Videos
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
4 Videos
Similar Questions
Knowledge Check
Two equi convex lenses each of focal lengths 20 cm and refractive index 1.5 are placed in & contact and space between them is filled with water of refractive index 43. The combination works as
Aconverging lens of focal length 30 cmBdiverging lens of focal length 15 cmCconverging lens of focal length 15 cmDdiverging lens of focal length 40 cmFind the change in the focal lengthof the lens, if a convex lens of focal length 20cm and refractive index 1.5, is immersed in water having refractive index 1.33.
A62.2cmB5.82cmC58.2cmD6.22cmA convex lens of focal length 10cm and concave lens of focal length 20cm are kept 5cm apart. The focal length of the equivalent lens is
A1203cmB18cmC30cmD403
Two identical equiconvex lenses of refractive index 3/2 and focal length 16 cm are kept in contact. The space between the lenses is filled with water of refractive index 4/3. What is the focal length of the combination ?
View SolutionFind the focal length of the lens shown in the Fig..
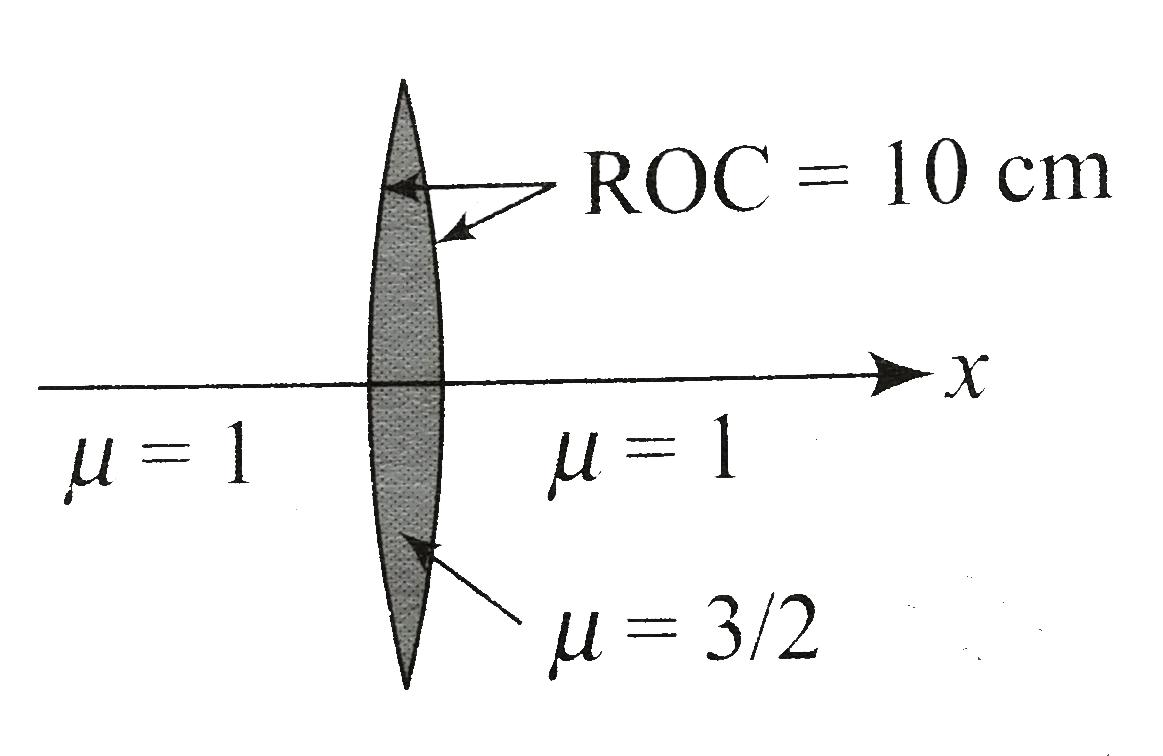
View SolutionFind the focal length of the lens shown in the Fig..

View SolutionA concave lens of focal length 12 cm and a convex lens of focal length 20 cm are kept in contact with each other .
Find the focal length of the combination .
View SolutionA convergent lens of focal length 20cm and made of a material with refractive index 1.1 is immersed in water. The lens will behave as a
View Solution