Doubtnut Promotions Sticky

For the function f(x)=xcosx1x,x≥1(A) for at least one x in the interval [1, c), f(x +2)-fx) 2 (B) lim f(x)= 1 (C) for all x in the interval [1, co), f(x +2)-f(x)> 2 (D) f (x) is strictly decreasing in the interval [1, co) lim fix )=

A

for atleast one x in the interval [1,∞),f(x+2)−f(x)<2

B

limx→∞f'(x)=1

C

for all x in the interval [1,∞),f(x+2)−f(x)>2

D

f'(x) is strictly decreasing in the interval [1,∞).

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B, C, D

Given, f(x) = xcos1x,x≥1⇒f'(x)=1xsin1x+cos1x
⇒ f''(x)=−1x3cos(1x)
Now, limx→∞f'(x)=0+1=1⇒ Option (b) is correct. Now, x∈(1,∞)⇒1x∈(0,1]⇒f''(x)<0
Option (d) is correct.
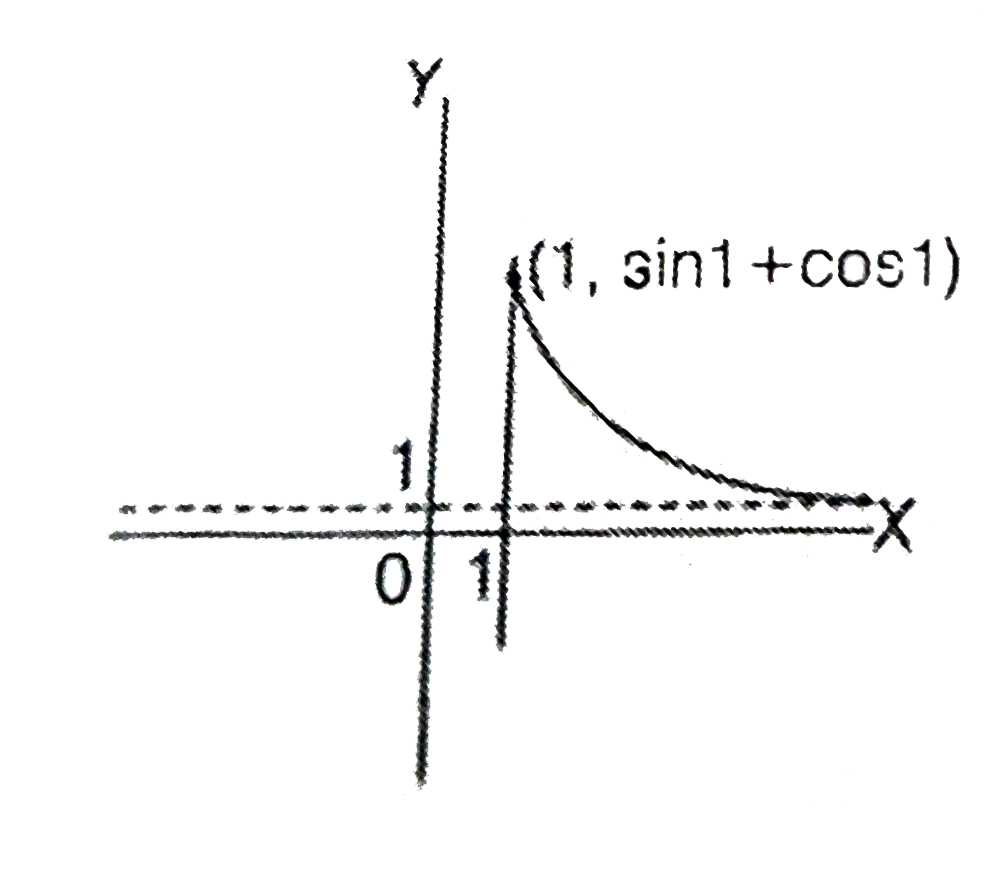
As f'(1) = sin 1 + cos 1>1
f'(x) is strictly decreasing and limx→∞f'(x)=1
So, graph of f'(x) is shown as below.
ocr_image Now, in [x,x+2],x∈[1,∞), f (x) is continuous and differentiable so by LMVT,
f'(x)=f(x+2)−f(x)2
As, f'(x)>1
For all x∈[1,∞)
⇒f(x+2)−f(x)2>1⇒f(x+2)−f(x)>2
For all x∈[1,∞)

|
Updated on:21/07/2023
Class 12MATHSLIMITS AND DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    The function f(x)=x2−2x is strictly increasing in the interval

    A(-2, -1)
    B(-1, 0)
    C(0, 1)
    D(1, 2)
  • Question 2 - Select One

    In the interval (0,1),f(x)=x2–x+1 is -

    Amonotonic
    Bnot monotonic
    Cdecreasing
    Dincreasing
  • Question 3 - Select One

    The function f(x)=2x3+3x2−12x+1 decreases in the interval

    A(2,3)
    B(1,2)
    C(−2,1)
    D(−3,−2)