Question

Let ${\displaystyle f:R\to R\text{and}g:R\to R}$ be respectively given by ${\displaystyle f\left(x\right)=\left|x\right|+1\text{and}g\left(x\right)=x^2+1}$. Define ${\displaystyle h:R\to R}$ by ${\displaystyle h\left(x\right)=\{max\{f\left(x\right),g\left(x\right)\},ifx\le 0\text{and}min\{f\left(x\right),g\left(x\right)\},ifx>0}$.The number of points at which ${\displaystyle h\left(x\right)}$ is not differentiable is

Answer

3

Explanation

PLAM
(i) In these type of questions, we draw the graph of the function.
(ii) The points at which the curve taken a sharp turn. Are the points of non-differentiability.
Curve of f (x) and g (x) are

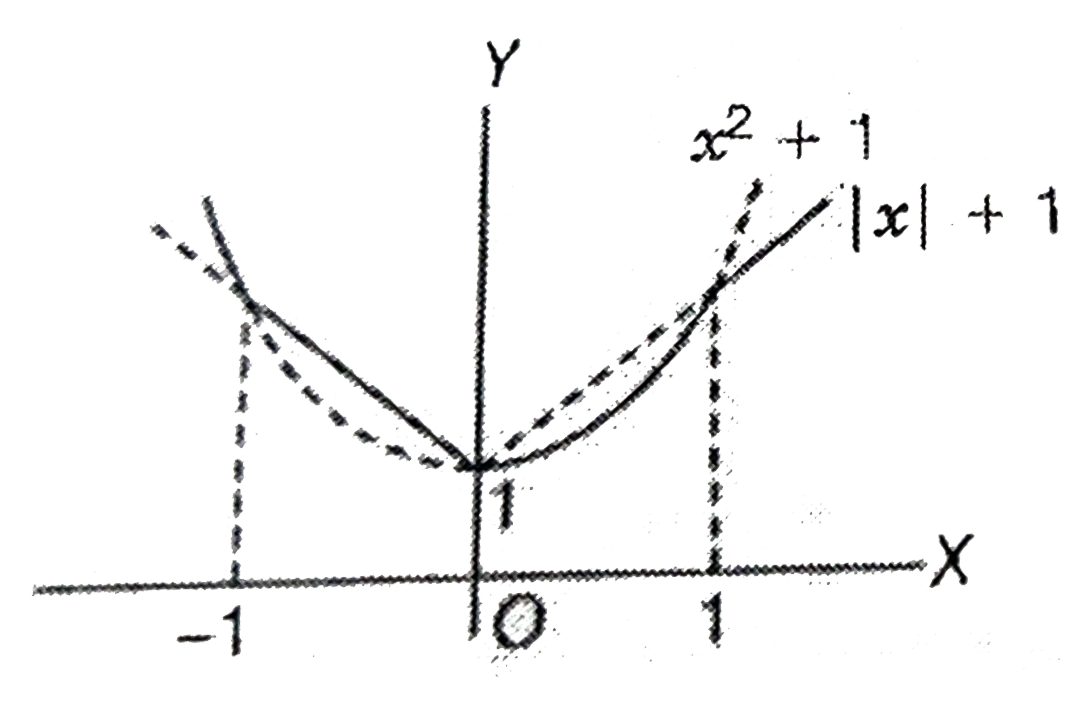
h (x) is not differentiable at `x = pm 1 and 0`.
As, h(x) take sharp turns at ` x = pm 1 and 0`.
Hence, number of points of non-differentiability of h (x) is 3.